頂角為36°的等腰三角形被稱為黃金三角形，在∠A=36°的△ABC中，AB=AC，BD是∠ABC的角平分線，交AC于D，若AC=4cm,則BC=2（5-1）2（5-1）cm.
5
5
【考點(diǎn)】黃金分割；相似三角形的性質(zhì)．
【答案】2（-1）
5
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/17 20:30:2組卷：160引用：2難度：0.5
相似題
-
1．已知線段AB=10cm,點(diǎn)C是線段AB的黃金分割點(diǎn)（AC＞BC），則AC的長(zhǎng)為（ ）
發(fā)布：2025/6/21 1:30:2組卷：1171引用：13難度：0.9 -
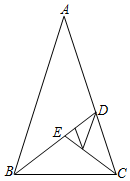2．如果一個(gè)等腰三角形的頂角為36°，那么可求其底邊與腰之比等于，我們把這樣的等腰三角形稱為黃金三角形．如圖，在△ABC中，AB=AC=1，∠A=36°，△ABC看作第一個(gè)黃金三角形；作∠ABC的平分線BD，交AC于點(diǎn)D，△BCD看作第二個(gè)黃金三角形；作∠BCD的平分線CE，交BD于點(diǎn)E，△CDE看作第三個(gè)黃金三角形；……以此類推，第2020個(gè)黃金三角形的腰長(zhǎng)是（ ）5-12發(fā)布：2025/6/20 23:30:1組卷：358引用：2難度：0.5 -
3．如圖，在△ABC中，點(diǎn)D在邊AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．
（1）求∠B的度數(shù)；
（2）我們把有一個(gè)內(nèi)角等于36°的等腰三角形稱為黃金三角形．它的腰長(zhǎng)與底邊長(zhǎng)的比（或者底邊長(zhǎng)與腰長(zhǎng)的比）等于黃金比．5-12
①寫出圖中所有的黃金三角形，選一個(gè)說(shuō)明理由；
②求AD的長(zhǎng)；
③在直線AB或BC上是否存在點(diǎn)P（點(diǎn)A、B除外），使△PDC是黃金三角形？若存在，在備用圖中畫出點(diǎn)P，簡(jiǎn)要說(shuō)明畫出點(diǎn)P的方法（不要求證明）；若不存在，說(shuō)明理由．
發(fā)布：2025/6/16 21:0:1組卷：865引用：3難度：0.5
相關(guān)試卷