如圖，在△ABC中，點D在邊AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．
（1）求∠B的度數；
（2）我們把有一個內角等于36°的等腰三角形稱為黃金三角形．它的腰長與底邊長的比（或者底邊長與腰長的比）等于黃金比5-12．
①寫出圖中所有的黃金三角形，選一個說明理由；
②求AD的長；
③在直線AB或BC上是否存在點P（點A、B除外），使△PDC是黃金三角形？若存在，在備用圖中畫出點P，簡要說明畫出點P的方法（不要求證明）；若不存在，說明理由．
5
-
1
2
【考點】黃金分割．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：864引用：3難度：0.5
相似題
-
1．若點C是線段AB的黃金分割點，且AC=2，則AB=
．發布：2025/6/7 18:30:1組卷：251引用：3難度：0.9 -
2．在小提琴的設計中，經常會引入黃金分割的概念．如圖，一架小提琴中AC、BC、AB各部分長度的比滿足，長久以來，很多人認為ACBC=BCAB=5-12是個很特別的數，若5-12介于兩個連續（相鄰）的整數a與b（a＜b）之間，則3a+4b的算術平方根為 ．5-12發布：2025/6/7 14:0:1組卷：54引用：1難度：0.6 -
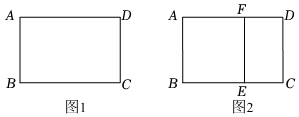3．閱讀理解：二次根式的除法，要化去分母中的根號，需將分子、分母同乘以一個恰當的二次根式．
例如：化簡．13-2
解：將分子、分母同乘以得：3+2．13-2=3+2（3-2）（3+2）=3+2
拓展延伸：
寬與長的比是的矩形叫黃金矩形．如圖1，已知黃金矩形ABCD的寬5-12．AB=2
（1）求黃金矩形ABCD中BC邊的長；
（2）如圖2，將圖1中的黃金矩形裁剪掉一個以AB為邊的正方形ABEF，得到新的矩形DCEF，猜想矩形DCEF是否為黃金矩形，并證明你的結論．發布：2025/6/7 7:0:1組卷：287引用：4難度：0.5