當(dāng)光線經(jīng)過鏡面反射時(shí),入射光線、反射光線與鏡面所夾的角對應(yīng)相等,你可用這一結(jié)論解答下列問題:
(1)在圖(1)中潛望鏡的兩面鏡子AB∥CD,光線經(jīng)過鏡子反時(shí),∠1=∠2,∠3=∠4,則進(jìn)入潛望鏡的光線EF和離開潛望鏡的光線GH是平行的,請說明理由;
(2)如圖(2),改變兩平面鏡AB、CD之間的位置,若鏡子AB與BC的夾角∠ABC=α,經(jīng)過兩次反射后,∠1=∠2,∠3=∠4,仍可以使入射光線EF與反射光線GH平行但方向相反.則α的度數(shù)為 90°90°(直接寫出答案).
(3)拓展應(yīng)用:如圖(3),若鏡子AB與BC的夾角α=110°,鏡子CD與BC的夾角∠BCD=β(90°<β<180°),入射光線EF與鏡面AB的夾角∠1=30°,已知入射光線EF從鏡面AB開始反射,經(jīng)過n(n為正整數(shù),且n≤3)次反射,當(dāng)?shù)趎次反射光線與入射光線EF平行時(shí),求β的度數(shù).

【考點(diǎn)】平行線的判定與性質(zhì);列代數(shù)式.
【答案】90°
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:213引用:1難度:0.4
相似題
-
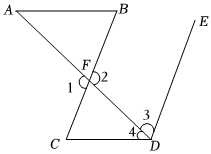 1.請把推理過程補(bǔ)充完整:
1.請把推理過程補(bǔ)充完整:
如圖,∠1+∠3=180°,∠CDE+∠B=180°,求證:∠A=∠4.
證明:∵∠1=∠2(依據(jù)1:);
又∠1+∠3=180°,
∴∠2+∠3=180°,
∴∥(依據(jù)2:);
∴∠CDE+=180°(依據(jù)3:);
又∠CDE+∠B=180°,
∴∠B=∠C;
∴AB∥CD(依據(jù)4:);
∴∠A=∠4(依據(jù)5:).發(fā)布:2025/6/8 4:30:1組卷:65引用:1難度:0.6 -
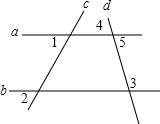 2.已知:如圖,∠1=∠2.求證:∠3+∠4=180°
2.已知:如圖,∠1=∠2.求證:∠3+∠4=180°
證明:∵∠1=∠2
∴a∥b ()
∴∠3+∠5=180° ()
又∵∠4=∠5()
∴∠3+∠4=180°發(fā)布:2025/6/8 3:30:1組卷:158引用:2難度:0.8 -
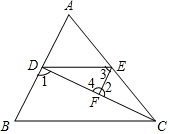 3.完成下面的證明:
3.完成下面的證明:
如圖,已知∠1、∠2互為補(bǔ)角,且∠3=∠B,
求證:∠AED=∠ACB.
證明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 ()
∴AB∥EF()
∴∠3=()
又∠3=∠B
∴∠B=()
∴DE∥BC ()
∴∠AED=∠ACB ()發(fā)布:2025/6/8 4:0:1組卷:766引用:9難度:0.6


