如圖是某公園一噴水池，在水池中央有一垂直于地面的噴水柱，噴水時，水流在各方向沿形狀相同的拋物線落下．若水流噴出的高度y（m）與水平距離x（m）之間的函數關系式為y=-（x-1）2+2.25．
（1）求噴出的水流離地面的最大高度；
（2）求噴嘴離地面的高度；
（3）若把噴水池改成圓形，那么水池半徑至少為多少時，才能使噴出的水流不落在水池外？
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/7 21:0:8組卷：883引用：13難度：0.5
相似題
-
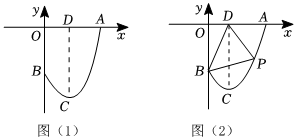1．如圖（1），一塊鋼板余料截面的兩邊為線段OA，OB，另一邊曲線ACB為拋物線的一部分，其中C點為拋物線的頂點，CD⊥OA于D，以OA邊所在直線為x軸，OB邊所在直線為y軸，建立平面直角坐標系xOy,規定一個單位代表1米．已知OD=1米，DA=2米，CD=4米．
（1）求曲線ACB所在拋物線的函數表達式；
（2）若在該鋼板余料中截取一個一邊長為3米的矩形，設該矩形的另一邊長為h米，求h的取值范圍；
（3）如圖（2），若在該鋼板余料中截取一個△PBD，其中點P在拋物線ACB上，記△PBD的面積為S，求S的最大值．發布：2025/5/23 16:0:1組卷：103引用：1難度：0.5 -
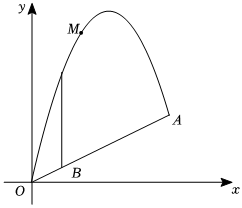2．如圖，一小球M從斜坡OA上的O點處拋出，建立如圖所示的平面直角坐標系，球的拋出路線是拋物線L1：y=-+bx的一部分，斜坡可以看作直線L2：y=12x2x的一部分．若小球經過點（6，6），解答下列問題：12
（1）求拋物線L1的表達式，并直接寫出拋物線L1的對稱軸；
（2）小球在斜坡上的落點為A，求A點的坐標；
（3）在斜坡OA上的B點有一棵樹，B點的橫坐標為2，樹高為4，小球M能否飛過這棵樹？通過計算說明理由；
（4）直接寫出小球M在飛行的過程中離斜坡OA的最大高度．發布：2025/5/23 16:30:1組卷：329引用：3難度：0.5 -
3．【綜合實踐】
某公園在人工湖里安裝一個噴泉，在湖心處豎直安裝一根水管，在水管的頂端安一個噴水頭，噴出的水柱形狀可以看作是拋物線的一部分．若記水柱上某一位置與水管的水平距離為x米，與湖面的垂直高度為y米．下面的表中記錄了x與y的五組數據：
（1）在下面網格（圖1）中建立適當的平面直角坐標系，并根據表中所給數據畫出表示y與x函數關系的圖象；x（米） 0 1 2 3 4 y（米） 0.5 1.25 1.5 1.25 0.5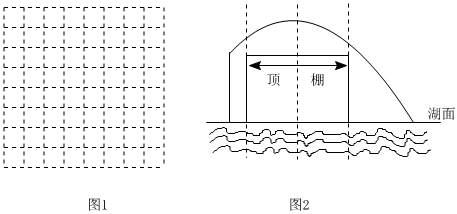 
（2）若水柱最高點距離湖面的高度為m米，則m=，并求y與x函數表達式；
（3）現公園想通過噴泉設立新的游玩項目，準備通過只調節水管露出湖面的高度，使得游船能從拋物線形水柱下方通過，如圖2所示，為避免游船被噴泉淋到，要求游船從拋物線形水柱下方中間通過時，頂棚上任意一點到水柱的豎直距離均不小于0.5米，已知游船頂棚寬度為3米，頂棚到湖面的高度為2米，那么公園應將水管露出湖面的高度（噴水頭忽略不計）至少調節到多少米才能符合要求？請通過計算說明理由（結果保留一位小數）．發布：2025/5/23 16:30:1組卷：1253引用：4難度：0.5