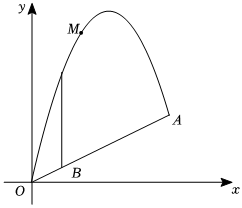
如圖，一小球M從斜坡OA上的O點處拋出，建立如圖所示的平面直角坐標系，球的拋出路線是拋物線L1：y=-12x2+bx的一部分，斜坡可以看作直線L2：y=12x的一部分．若小球經過點（6，6），解答下列問題：
（1）求拋物線L1的表達式，并直接寫出拋物線L1的對稱軸；
（2）小球在斜坡上的落點為A，求A點的坐標；
（3）在斜坡OA上的B點有一棵樹，B點的橫坐標為2，樹高為4，小球M能否飛過這棵樹？通過計算說明理由；
（4）直接寫出小球M在飛行的過程中離斜坡OA的最大高度．
1
2
x
2
1
2
【考點】二次函數的應用．
【答案】（1）；x=4；
（2）；
（3）小球M能飛過這棵樹，理由見解析；
（4）．
y
=
-
1
2
x
2
+
4
x
（2）
（
7
，
7
2
）
（3）小球M能飛過這棵樹，理由見解析；
（4）
49
8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/23 16:30:1組卷：330引用：3難度：0.5
相似題
-
1．如圖，某隧道口的橫截面是拋物線形，已知路寬AB為6米，最高點離地面的距離OC為5米．以最高點O為坐標原點，拋物線的對稱軸為y軸，1米為數軸的單位長度，建立平面直角坐標系，
求：（1）以這一部分拋物線為圖象的函數解析式，并寫出x的取值范圍；
（2）有一輛寬2.8米，高1米的農用貨車（貨物最高處與地面AB的距離）能否通過此隧道？發布：2025/5/28 6:0:2組卷：1005引用：17難度：0.1 -
2．周長是4m的矩形，它的面積S（m2）與一邊長x（m）的函數圖象大致是（ ）
發布：2025/5/28 4:30:1組卷：1057引用：5難度：0.5 -
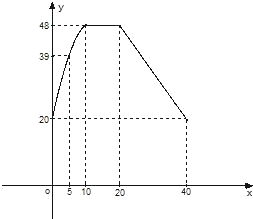3．通過實驗研究，專家們發現：初中學生聽課的注意力指標數是隨著老師講課時間的變化而變化的，講課開始時，學生的興趣激增，中間有一段時間的興趣保持平穩狀態，隨后開始分散．學生注意力指標數y隨時間x（分鐘）變化的函數圖象如圖所示（y越大表示注意力越集中）．當0≤x≤10時，圖象是拋物線的一部分，當10≤x≤20和20≤x≤40時，圖象是線段．
（1）當0≤x≤10時，求注意力指標數y與時間x的函數關系式；
（2）一道數學綜合題，需要講解24分鐘．問老師能否經過適當安排，使學生聽這道題時，注意力的指標數都不低于36？發布：2025/5/28 10:30:1組卷：308引用：33難度：0.1