觀察以下等式：
第1個等式：（2×1+1）2=（2×2+1）2-（2×2）2
第2個等式：（2×2+1）2=（3×4+1）2-（3×4）2
第3個等式：（2×3+1）2=（4×6+1）2-（4×6）2
第4個等式：（2×4+1）2=（5×8+1）2-（5×8）2
按照以上規律，解決下列問題：
（1）寫出第5個等式：（2×5+1）2=（6×10+1）2-（6×10）2（2×5+1）2=（6×10+1）2-（6×10）2．
（2）直接寫出你猜想的第n個等式（用含n的式子表示） （2n+1）2=[（n+1）×2n+1]2-[（n+1）×2n]2．（2n+1）2=[（n+1）×2n+1]2-[（n+1）×2n]2．．
【答案】（2×5+1）2=（6×10+1）2-（6×10）2；（2n+1）2=[（n+1）×2n+1]2-[（n+1）×2n]2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 22:30:1組卷：150引用：1難度：0.5
相似題
-
1．觀察下列各個等式的規律：
第一個等式：=1，第二個等式：22-12-12=2，第三個等式：32-22-12=3…42-32-12
請用上述等式反映出的規律解決下列問題：
（1）直接寫出第四個等式；
（2）猜想第n個等式（用n的代數式表示），并證明你猜想的等式是正確的．發布：2025/5/30 21:0:1組卷：1641引用：22難度：0.5 -
2．已知（n≥2），且n是自然數，對n2進行如下“分裂”，可分裂成連續奇數的和：22=1+3，32=1+3+5，…，以此規律，將20212可以分裂成 個奇數的和，n2分裂的數中最大的數是 （用含n的代數式表示）．
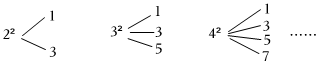發布：2025/5/30 19:30:1組卷：84引用：2難度：0.5 -
3．一列有規律的數：-1，-4，7，10，-13，-16，19，22…則這列數的第2023個數為（ ）
發布：2025/5/30 20:0:1組卷：272引用：1難度：0.6