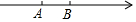如圖，數(shù)軸上有兩點A，B，表示的數(shù)分別是m,n.已知m,n是兩個連續(xù)的整數(shù)，且m+n=-1，則分式m2-2mm-1÷m21-m的值為（ ）
m
2
-
2
m
m
-
1
m
2
1
-
m
【考點】分式的化簡求值．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/5/27 14:0:0組卷：480引用：5難度：0.7
相似題
-
1．（1）計算：（π-3）0+（
）-2-2cos30°+|1-12|．3
（2）先化簡，再求值：÷（1+x+2x2-2x+1），其中x=3x-1+1．2發(fā)布：2025/6/8 14:0:2組卷：225引用：2難度：0.5 -
2．先化簡，再求值：
，其中a是已知兩邊分別為2和3的三角形的第三邊長，且a是整數(shù)．（aa+2+9-4aa2-4）÷a-3a-2發(fā)布：2025/6/8 15:0:1組卷：310引用：3難度：0.7 -
3．同學們已經(jīng)學習了分式，整式還有二次根式．小明發(fā)現(xiàn)像m+n,mnp,
等代數(shù)式，如果任意交換兩個字母的位置，式子的值都不變．太神奇了!于是他把這樣的式子命名為神奇對稱式．他還發(fā)現(xiàn)像m2+n2，（m-1）（n-1）等神奇對稱式都可以用mn,m+n表示．例如：m2+n2=（m+n）2-2mn,（m-1）（n-1）=mn-（m+n）+1．于是小明把mn和m+n稱為基本神奇對稱式．m2+n2
請根據(jù)以上材料解決下列問題：
（1）代數(shù)式①，②m2-n2，③2mn，④nm（x≥0，y≥0，z≥0）中，屬于神奇對稱式的是 （填序號）；xy+yz+xz
（2）已知（x-m）（x-n）=x2-px+q.
①若p=3，q=-2，則神奇對稱式=；1m+1n
②若，求神奇對稱式p2-q=0的最小值．m3+1m+n3+1n發(fā)布：2025/6/8 19:30:1組卷：85引用：1難度：0.6