閱讀理解，在平面直角坐標系中，P1（x1，y1），P2（x2，y2），如何求P1，P2的距離？
如圖1，作Rt△P1P2Q，在Rt△P1P2Q中，P1P22=P1Q2+P2Q2=（x2-x1）2+（y2-y1）2，所以P1P2=（x2-x1）2+（y2-y1）2．因此，我們得到平面上兩點P1（x1，y1），P2（x2，y2）之間的距離公式為P1P2=（x2-x1）2+（y2-y1）2．
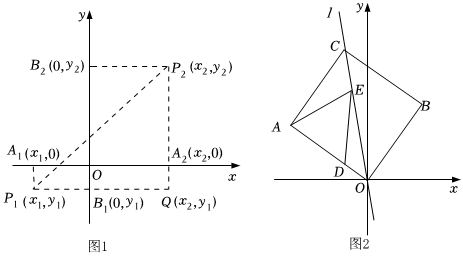
根據上面得到的公式，解決下列問題：
（1）已知平面上兩點A（-3，4），B（5，10），求AB的距離；
（2）若平面上有三個點A（-2，1），B（1，2），C（-1，3），試判斷△ABC的形狀，并說明理由；
（3）如圖2，在正方形AOBC中，點A（-4，3），點D在OA邊上，且D（-1，34），直線l經過O，C兩點，點E是直線l上的一個動點，求DE+EA的最小值．
P
1
P
2
2
=
P
1
Q
2
+
P
2
Q
2
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
P
1
P
2
=
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
P
1
P
2
=
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
D
（
-
1
，
3
4
）
【答案】（1）10；
（2）△ABC是等腰直角三角形；
（3）．
（2）△ABC是等腰直角三角形；
（3）
5
17
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/19 8:0:9組卷：107引用：1難度：0.4
相似題
-
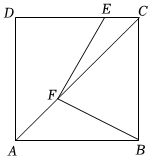1．如圖，正方形ABCD的邊長是4，點E在DC上，點F在AC上，∠BFE=90°，若CE=1．則AF的長為 ．發布：2025/5/30 8:0:2組卷：1134引用：3難度：0.4 -
2．在正方形ABCD中，M是對角線BD上的一點，點E在AD的延長線上，連接AM、EM、CM，延長EM交邊AB于點F，若AM=EM，∠E=30°，則下列結論：
①FM=ME；
②BF=DE；
③CM⊥EF；
④，其中正確的結論序號是 ．2BF+MD=BC發布：2025/5/30 15:0:2組卷：393引用：4難度：0.3 -
3．如圖，在正方形ABCD中，AC是對角線，點E是AD的中點，點F在AC上，若∠EBF=45°，，則線段BE的長為 ．CF=22發布：2025/5/30 14:0:1組卷：39引用：1難度：0.4