在正方形ABCD中，M是對角線BD上的一點，點E在AD的延長線上，連接AM、EM、CM，延長EM交邊AB于點F，若AM=EM，∠E=30°，則下列結論：
①FM=ME；
②BF=DE；
③CM⊥EF；
④
2
BF
+
MD
=
BC
，其中正確的結論序號是
①②③
①②③
．

【答案】①②③

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。

發(fā)布：2025/5/30 15:0:2組卷：394引用：4難度：0.3

相似題

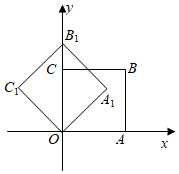1．如圖，在平面直角坐標系中，將正方形OABC繞點O逆時針旋轉45°后得到正方形OA₁B₁C₁，依此方式，繞點O連續(xù)旋轉2022次得到正方形OA₂₀₂₂B₂₀₂₂C₂₀₂₂，如果點A的坐標為（1，0），那么點B₂₀₂₂的坐標為（　　）
A．（1，-1） B．（0，
2
） C．（
2
，0） D．（-1，1）
發(fā)布：2025/5/31 15:30:1組卷：223引用：7難度：0.5
解析
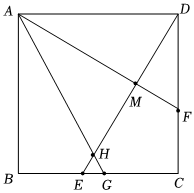2．如圖，在正方形ABCD中，點E在BC上，點F在CD上，AF⊥DE于點M，點H在EM上，MH=MD，連接AH延長交BC于點G，若CF=6，CG=7，則線段DE的長為
．
發(fā)布：2025/5/31 22:30:1組卷：424引用：6難度：0.4
解析
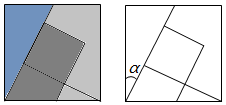3．五巧板是七巧板的變形，也是由一個正方形分割而成的，圖中與∠α互余的角有
個．
發(fā)布：2025/5/31 21:0:1組卷：235引用：3難度：0.5
解析

相關試卷

在正方形ABCD中，M是對角線BD上的一點，點E在AD的延長線上，連接AM、EM、CM，延長EM交邊AB于點F，若AM=EM，∠E=30°，則下列結論：①FM=ME；②BF=DE；③CM⊥EF；④2BF+MD=BC，其中正確的結論序號是 ①②③①②③．