當(dāng)前位置:
2020-2021學(xué)年廣東省韶關(guān)市武江區(qū)北江實(shí)驗(yàn)中學(xué)九年級(jí)(上)期末數(shù)學(xué)試卷>
試題詳情
新冠肺炎期間,某超市將購(gòu)進(jìn)一批口罩進(jìn)行銷售,已知購(gòu)進(jìn)4盒甲口罩和6盒乙口罩需260元,購(gòu)進(jìn)5盒甲口罩和4盒乙口罩需220元.兩種口罩以相同的售價(jià)銷售,當(dāng)售價(jià)為40元時(shí),乙口罩可銷售100盒,售價(jià)每提高1元,乙口罩少銷售5盒.
(1)求甲、乙兩種口罩每盒的進(jìn)價(jià)分別為多少元?
(2)當(dāng)乙口罩的售價(jià)為多少元時(shí),乙口罩的銷售總利潤(rùn)最大?
【考點(diǎn)】二次函數(shù)的應(yīng)用;二元一次方程組的應(yīng)用.
【答案】(1)甲、乙兩種口罩每盒的進(jìn)價(jià)分別為20元、30元;
(2)1125元.
(2)1125元.
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/6/3 5:30:1組卷:12引用:2難度:0.4
相似題
-
1.根據(jù)以下信息,探索完成任務(wù).
如何設(shè)計(jì)種植方案? 素材1 小明以“種植農(nóng)作物”為主題在自己家100平方米的土地上進(jìn)行課外實(shí)踐,現(xiàn)有A、B兩種作物的相關(guān)信息如下表所示: A作物 B作物 每平方米種植株樹(株) 2 10 單株產(chǎn)量(千克) 1.2 0.5 素材2 由于A作物植株間距較大,可增加A作物每平方米的種植株樹.經(jīng)過調(diào)研發(fā)現(xiàn),每平方米種植A作物每增加1株,A作物的單株產(chǎn)量減少0.1千克. 素材3 若同時(shí)種植A、B兩種作物,實(shí)行分區(qū)域種植. 問題解決 單一種植(全部種植A作物) 任務(wù)1:明確數(shù)量關(guān)系 設(shè)每平方米增加x株A作物(x為正整數(shù)),則每平方米有 株,單株產(chǎn)量為
千克. (用含x的代數(shù)式表示)任務(wù)2:計(jì)算產(chǎn)量 要使A作物每平方米產(chǎn)量為4.8千克,則每平方米應(yīng)種植多少株? 分區(qū)種植(種植A、B兩種作物) 任務(wù)3:規(guī)劃種植方案 設(shè)這100平方米的土地中有a平方米用于種植A作物,且每平方米產(chǎn)量最大,其余區(qū)域按照每平方米10株種植B作物,當(dāng)這100平方米總產(chǎn)量不低于496千克時(shí),則a的取值范圍是 . 發(fā)布:2025/6/4 1:0:1組卷:1106引用:8難度:0.5 -
2.對(duì)于豎直向上拋出的物體,在不考慮空氣阻力的情況下,有如下的關(guān)系式:
,其中h是物體上升的高度,v是拋出時(shí)的速度,g是重力加速度(g≈10m/s2),t是拋出后的時(shí)間.如果一物體以25m/s的初速度從地面豎直向上拋出,經(jīng)過 秒鐘后它在離地面20m高的地方.h=vt-12gt2發(fā)布:2025/6/4 22:0:2組卷:133引用:2難度:0.6 -
3.數(shù)學(xué)活動(dòng)課上,老師提出一個(gè)探究問題:
制作一個(gè)體積為10dm3,底面為正方形的長(zhǎng)方體包裝盒,當(dāng)?shù)酌孢呴L(zhǎng)為多少時(shí),需要的材料最省(底面邊長(zhǎng)不超過3dm,且不考慮接縫).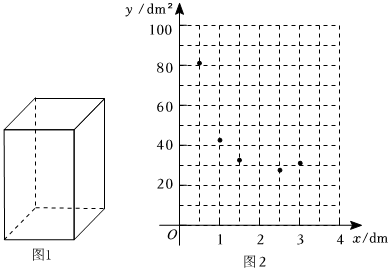
某小組經(jīng)討論得出:材料最省,就是盡可能使得長(zhǎng)方體的表面積最小.
下面是他們的探究過程,請(qǐng)補(bǔ)充完整:
(1)設(shè)長(zhǎng)方體包裝盒的底面邊長(zhǎng)為x dm,表面積為y dm2.
可以用含x的代數(shù)式表示長(zhǎng)方體的高為.10x2dm
根據(jù)長(zhǎng)方體的表面積公式:長(zhǎng)方體表面積=2×底面積+側(cè)面積.
得到y(tǒng)與x的關(guān)系式:(0<x≤3);
(2)列出y與x的幾組對(duì)應(yīng)值:
(說明:表格中相關(guān)數(shù)值精確到十分位)x/dm … 0.5 1.0 1.5 2.0 2.5 3.0 y/dm2 … 80.5 42.0 31.2 a 28.5 31.3
表中a=.
(3)在圖2的平面直角坐標(biāo)系xOy中,描出以補(bǔ)全后的表中各對(duì)對(duì)應(yīng)值為坐標(biāo)的點(diǎn),畫出該函數(shù)的圖象:
(4)結(jié)合畫出的函數(shù)圖象,解決問題:
長(zhǎng)方體包裝盒的底面邊長(zhǎng)約為 dm時(shí),需要的材料最省;當(dāng)長(zhǎng)方體包裝盒表面積為30dm2時(shí),底面邊長(zhǎng)約為 dm.發(fā)布:2025/6/4 16:0:1組卷:288引用:4難度:0.4


