在數軸上，點A表示的數為1，點B表示的數為3．對于數軸上的圖形M，給出如下定義：P為圖形M上任意一點，Q為線段AB上任意一點，如果線段PQ的長度有最小值，那么稱這個最小值為圖形M關于線段AB的極小距離，記作d1（M，線段AB）；如果線段PQ的長度有最大值，那么稱這個最大值為圖形M關于線段AB的極大距離，記作d2（M，線段AB）．
例如：點K表示的數為4，則d1（點K，線段AB）=1，d2（點K，線段AB）=3．
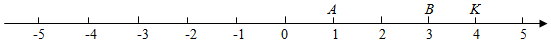
已知點O為數軸原點，點C，D為數軸上的動點．
（1）d1（點O，線段AB）=11，d2（點O，線段AB）=33；
（2）若點C，D表示的數分別為m,m+2，d1（線段CD，線段AB）=2．求m的值；
（3）點C從原點出發，以每秒2個單位長度沿x軸正方向勻速運動；點D從表示數-2的點出發，第1秒以每秒2個單位長度沿x軸正方向勻速運動，第2秒以每秒4個單位長度沿x軸負方向勻速運動，第3秒以每秒6個單位長度沿x軸正方向勻速運動，第4秒以每秒8個單位長度沿x軸負方向勻速運動，…，按此規律運動，C，D兩點同時出發，設運動的時間為t秒，若d2（線段CD，線段AB）小于或等于6，直接寫出t的取值范圍．（t可以等于0）
【答案】1；3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：1113引用：6難度：0.4
相似題
-
1．某中學租用兩輛小汽車（速度相同）同時送1名帶隊老師和7名七年級學生到市區參加數學競賽．每輛車限坐4人（不包括司機），其中一輛小汽車在距離考場15千米的地方出現故障，此時離截止進考場時刻還有42分鐘，這時唯一可利用的只有另一輛小汽車，且這輛車的平均速度是60千米/時，人步行速是5千米/時．（人上下車的時間不計）
（1）若小汽車送4人到達考場后再返回到出故障處接其他4人．請你通過計算說明能否在截止進考場的時刻前到達考場？
（2）帶隊老師提出一種方案：先將4人用車送到考場，另外4人同時步行前往考場，小汽車到達考場后返回再接步行的4人到達考場．請你通過計算說明方案的可行性．
（3）所有學生、老師都到達考場，最少需要多少時間？發布：2025/5/29 6:30:1組卷：213引用：3難度：0.5 -
2．如圖，在矩形ABCD中，AB=12cm,BC=6cm.點P沿AB邊從點A開始向點B以2cm/s的速度移動；點Q沿DA邊從點D開始向點A以1cm/s的速度移動．如果P、Q同時出發，用t（s）表示移動的時間（0≤t≤6）那么：
（1）當t為何值時，△QAP為等腰直角三角形？
（2）求四邊形QAPC的面積，提出一個與計算結果有關的結論；
（3）當t為何值時，以點Q、A、P為頂點的三角形與△ABC相似？發布：2025/5/29 6:30:1組卷：1571引用：72難度：0.1 -
3．足球比賽的記分規則為：勝一場得3分，平一場得1分，負一場記0分，一個隊打了20場比賽，平了5場，共得32分，那么該隊勝場．
發布：2025/5/29 6:0:1組卷：113引用：6難度：0.5