【理解概念】
1．如果一條直線將一個圖形分割成面積相等的兩個部分，則稱這條直線叫做該圖形的“等積線”．
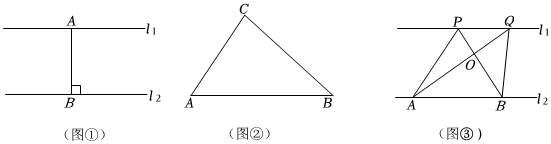
2．如圖①，直線l1∥l2，點A是直線l1上的一點，AB⊥l2，垂足為B，則線段AB的長度是l1與l2之間的距離．我們知道，兩條平行線之間的距離處處相等．
【新知探究】
（1）如圖②，過點A畫出△ABC的等積線，并簡要說明畫法；
（2）如圖③，直線l1∥l2，A、B是l2上的兩點，P、Q是l1上的兩點，分別連接AP、AQ、BP、BQ，AQ與BP交于點O．設△APO的面積為S1，△BQO的面積為S2，則S1==S2（填“＞”“＜”或“=”）．
【拓展提高】
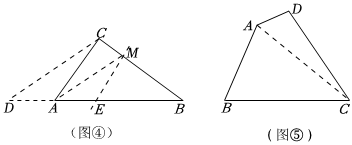
（1）如圖④，點M是△ABC中BC邊上的一點，CM＜BM．小峰同學做了如下的操作：
①連接MA，過點C畫CD∥MA，交BA的延長線于點D；
②找出線段BD的中點E，畫直線ME．
小峰認為直線ME就是△ABC的等積線，你同意嗎？說明理由．
（2）如圖⑤，在四邊形ABCD中，連接AC，△ACD的面積小于△ABC的面積．
過點A畫四邊形ABCD的等積線，并簡要說明畫法，不需說理．
【答案】=
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：305引用：3難度：0.4
相似題
-
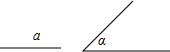1．（1）已知：線段a,∠α．求作：△ABC，使BC=a,∠C=∠B=∠α．（不寫作法，保留作圖痕跡）
（2）在（1）的圖形中，如果BC=6，∠α=30°，求△ABC的面積．3發布：2025/5/24 19:30:1組卷：61引用：2難度：0.7 -
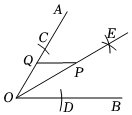2．如圖，已知∠AOB=60°．按以下步驟尺規作圖：
①以O點為圓心任意長為半徑畫弧分別交OA，OB于點C，D；
②分別以C、D兩點為圓心．大于CD長為半徑畫弧，兩段弧交于點E．并作射線OE；12
③在OE上任取一點P，過點P作PQ∥OB，交OA于點Q；
若點M在OB上，且滿足PM=PQ，則∠OMP的度數為（ ）發布：2025/5/24 19:30:1組卷：42引用：1難度：0.6 -
3．下面是小東設計的“過直線外一點作這條直線的平行線”的尺規作圖過程．
已知：直線l及直線l外一點P．
求作：直線PQ，使得PQ∥l.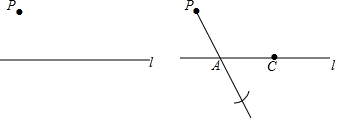
作法：如圖，
①在直線l上取一點A，作射線PA，以點A為圓心，AP長為半徑畫弧，交PA的延長線于點B；
②在直線l上取一點C（不與點A重合），作射線BC，以點C為圓心，CB長為半徑畫弧，交BC的延長線于點Q；
③作直線PQ．所以直線PQ就是所求作的直線．
根據小東設計的尺規作圖過程，
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：∵AB=，CB=，
∴PQ∥l（ ）（填推理的依據）．發布：2025/5/24 20:0:2組卷：1351引用：10難度：0.9