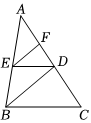
如圖，ED∥BC，BD是△ABC的平分線，EF平分∠AED交AC于點F，試說明EF∥BD．請補全推理過程，并在括號內填上相應的理由；
∵ED∥BC，
∴∠ABC=∠AED∠AED（ 兩直線平行，同位角相等兩直線平行，同位角相等）．
∵BD平分∠ABC，
∴∠ABD=12 ∠ABC∠ABC（ 角平分線的定義角平分線的定義）．
同理∠AEF=12∠AED12∠AED．
∴∠ABD=∠AEF∠AEF．
∴EF∥BD（ 同位角相等，兩直線平行同位角相等，兩直線平行）．
1
2
1
2
∠
AED
1
2
∠
AED
【答案】∠AED；兩直線平行，同位角相等；∠ABC；角平分線的定義；；∠AEF；同位角相等，兩直線平行
1
2
∠
AED
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 9:30:1組卷：134引用：4難度：0.7
相似題
-
1．如圖，在直角三角形ABC中，∠BAC=90°，將△ABC沿直線BC向右平移得到△DEF，連接AD，AE，下列結論：①AC∥DF；②AD∥BE，AE=BE；③∠ABE=∠DEF；④ED⊥AC，其中正確的結論有（ ）發布：2025/6/6 5:0:1組卷：376引用：3難度：0.7 -
2．完成證明并寫出推理根據：已知，如圖，∠1=132°，∠ACB=48°，∠2=∠3，FH⊥AB于H．求證：CD⊥AB．
證明：∵∠1=132°，∠ACB=48°，
∴∠1+∠ACB=180°．
∴DE∥BC（ ）．
∴∠2=∠DCB（ ）．
又∵∠2=∠3，
∴∠3=∠DCB（ ），
∴HF∥DC（ ），
∴∠CDB=∠FHB（ ）．
又∵FH⊥AB（ ），
∴∠FHB=90°∴∠CDB=．
∴CD⊥AB（ ）．發布：2025/6/6 5:30:2組卷：25引用：1難度：0.6 -
3．如圖，已知A、B、C三點在同一直線上，∠1=∠2，∠D=∠3．
（1）說明BD∥CE的理由；
（2）若∠C=68°，∠DAC=52°，求∠DBE的度數．發布：2025/6/6 5:30:2組卷：536引用：8難度：0.3