當(dāng)前位置:
2022-2023學(xué)年黑龍江省哈爾濱市香坊區(qū)德強(qiáng)學(xué)校初中部六年級(jí)(上)診斷數(shù)學(xué)試卷(11月份)(五四學(xué)制)>
試題詳情
閱讀下列材料,然后解決問(wèn)題.
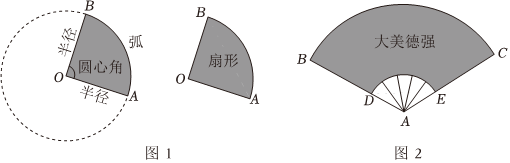
知識(shí)儲(chǔ)備:如圖1,圓上任意兩點(diǎn)間的部分叫做圓弧,簡(jiǎn)稱(chēng)弧.如弧AB.頂點(diǎn)在圓心的角,叫圓心角,如∠AOB.圓的一條弧和經(jīng)過(guò)這條弧的端點(diǎn)的兩條半徑所圍成的圖形叫做扇形.
理解分析:已知在同一個(gè)圓中,圓的面積公式S=πr2,因?yàn)閳A心角為1°的扇形共含有360個(gè),所以:扇形圓心角是1°時(shí),對(duì)應(yīng)的扇形面積列式為1360×πr2,扇形圓心角是2°時(shí),對(duì)應(yīng)的扇形面積列式為2360×πr2,扇形圓心角是3°時(shí),對(duì)應(yīng)的扇形面積列式為3360×πr2…,故扇形圓心角是n°時(shí),對(duì)應(yīng)的扇形面積列式為n360×πr2.
問(wèn)題:
(1)當(dāng)扇形圓心角是100°,半徑是6cm,扇形的面積為 10π10π平方厘米;(直接填空,結(jié)果保留π)
(2)根據(jù)材料所學(xué)知識(shí)解決問(wèn)題:如圖2,扇形紙扇完全打開(kāi)后,外側(cè)兩竹條AB,AC夾角為120°,AB的長(zhǎng)為30cm,扇面BD的長(zhǎng)為20cm,求扇面(陰影部分)的面積;(π取3)
(3)在德強(qiáng)學(xué)校一年一度的篝火晚會(huì)中,6年級(jí)15班同學(xué)準(zhǔn)備自制(2)中的紙扇參加演出.已知該班有男生20人,男生比女生的56少5人,全班同學(xué)都參加演出且每人需兩把紙扇.自制每把紙扇需要6根竹條,扇面的紙和書(shū)寫(xiě)“大美德強(qiáng)”的顏料若干,制作扇面時(shí)紙張有損耗,使用的面積和損耗的面積之比為4:1,此種紙張平均每平方分米0.5元,竹條每根0.1元,每把紙扇書(shū)寫(xiě)“大美德強(qiáng)”所需顏料的費(fèi)用比每把紙扇所需竹條總費(fèi)用的50%多0.1元,制作過(guò)程中每把紙扇平均還需其他費(fèi)用0.5元,請(qǐng)問(wèn)該班制作所有紙扇共需多少元錢(qián)?
1
360
×
π
r
2
2
360
×
π
r
2
3
360
×
π
r
2
n
360
×
π
r
2
5
6
【考點(diǎn)】圓的綜合題.
【答案】10π
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書(shū)面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/27 8:0:9組卷:51引用:2難度:0.5
相似題
-
1.已知:四邊形ABCD內(nèi)接于O,AC為⊙O的直徑,E為
中點(diǎn),連接AE、CE.?AB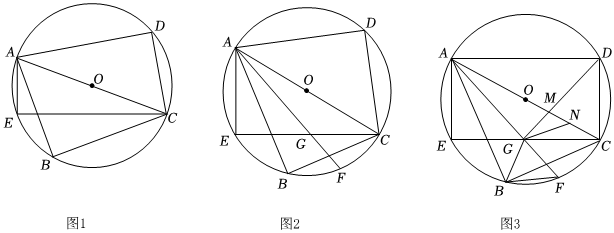
(1)如圖1,求證:2∠ACE+∠BAC=90°;
(2)如圖2,F(xiàn)為中點(diǎn),弦AF與CE交于點(diǎn)G,若G為EC中點(diǎn),求證:EC=2AE;?BC
(3)如圖3,在(2)的條件下,連接BG、DG,DG交AC于M,點(diǎn)N為MC上的點(diǎn),若∠AGD=90°,∠AFB=2∠MGN,MN=2,求線段BG的長(zhǎng).發(fā)布:2025/5/30 12:0:2組卷:68引用:1難度:0.3 -
2.如圖1,四邊形ABCD內(nèi)接于⊙O,AB=AC,AC⊥BD,垂足為點(diǎn)E.
(1)求證:∠BAC=2∠CAD;
(2)如圖2,點(diǎn)F在BD的延長(zhǎng)線上,且DF=DC,連接CF.求證:CF=CB;
(3)如圖3,在(2)的條件下,連接AF,當(dāng)AF=20,CF=時(shí),求⊙O的半徑長(zhǎng).85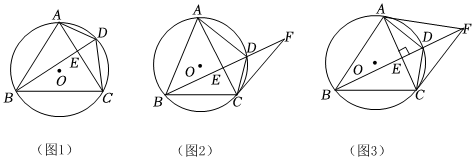 發(fā)布:2025/5/30 11:0:1組卷:314引用:1難度:0.4
發(fā)布:2025/5/30 11:0:1組卷:314引用:1難度:0.4 -
 3.閱讀下列材料,并回答問(wèn)題.
3.閱讀下列材料,并回答問(wèn)題.
[材料]自從《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022年版)》實(shí)施以來(lái),九年級(jí)的龍老師增加了一個(gè)習(xí)慣,就是在每個(gè)新章節(jié)備課時(shí)都會(huì)查閱新課標(biāo),了解該章知識(shí)的新舊課標(biāo)的變化,并在上課時(shí)告訴學(xué)生.他通過(guò)查閱新課標(biāo)獲悉:切線長(zhǎng)定理由“選學(xué)”改為“必學(xué)”,并新增“會(huì)過(guò)圓外的一個(gè)點(diǎn)作圓的切線”.在學(xué)習(xí)完《切線的性質(zhì)與判定》后,龍老師布置了一道課外思考題:“已知:如圖,⊙O及⊙O外一點(diǎn)P.求作:直線PM,使PM與⊙O相切于點(diǎn)M”.
班上小巖同學(xué)所在的學(xué)習(xí)小組經(jīng)過(guò)探索,給出了如下的一種作圖方法:
(1)連接OP,以O(shè)為圓心,OP長(zhǎng)為半徑作大圓O;
(2)若OP交小圓O于點(diǎn)N,過(guò)點(diǎn)N作小圓O的切線與大圓O交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B的上方);
(3)連接AO交小圓O于M,連接PM,則PM是小圓O的切線.
[問(wèn)題]
(1)請(qǐng)問(wèn)小巖同學(xué)所在的學(xué)習(xí)小組提供的作圖方法是否正確?請(qǐng)你按照步驟完成作圖(尺規(guī)作圖,保留作圖痕跡),并說(shuō)明理由.
(2)延長(zhǎng)AO交大圓O于C,連接CN,若OA=2,OM=1,求CN的長(zhǎng).發(fā)布:2025/5/30 11:30:2組卷:260引用:1難度:0.4


