探索規律，觀察下面算式，解答問題：
第1個等式：1=1²；
第2個等式：1+3=2²；
第3個等式：1+3+5=3²；
第4個等式：1+3+5+7=4²；
…
（1）按以上規律列出第5個等式
1+3+5+7+9=5²
1+3+5+7+9=5²
；
（2）請猜想1+3+5+7+9+…+（2n-1）=
n²
n²
；（n為正整數）；
（3）請用上述規律計算：61+63+65+…+97+99．

【答案】1+3+5+7+9=5²；n²

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/9/20 3:0:8組卷：153引用：2難度：0.5

相似題

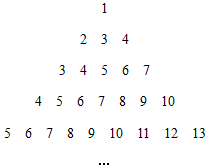1．將正整數按如圖方式進行有規律的排列，第2行最后一個數是4，第3行最后一個數是7，第4行最后一個數是10，…．按此規律，若2022是第m行第n個數，則m,n的值分別是（　　）
A．m=674，n=1346 B．m=674，n=1347
C．m=675，n=1348 D．m=675，n=1349
發布：2025/6/3 12:0:1組卷：520引用：2難度：0.6
解析
2．觀察下列各數：1，
4
3
，
9
7
，
16
15
，…，按你發現的規律計算這列數的第6個數為

．
發布：2025/6/3 11:30:1組卷：182引用：3難度：0.5
解析
3．已知：2+
2
3
=2²×
2
3
，3+
3
8
=3²×
3
8
，4+
4
15
=4²×
4
15
…，按此排列，則第10個等式是（　　）
A．10+
10
11
=10²×
10
11
B．10+
10
99
=10²×
10
99
C．11+
11
12
=11²×
11
12
D．11+
11
120
=11²×
11
120
發布：2025/6/3 11:0:2組卷：1152引用：4難度：0.5
解析

相關試卷

A．m=674，n=1346	B．m=674，n=1347
C．m=675，n=1348	D．m=675，n=1349

A．10+ 10 11 =10²× 10 11	B．10+ 10 99 =10²× 10 99
C．11+ 11 12 =11²× 11 12	D．11+ 11 120 =11²× 11 120

1．將正整數按如圖方式進行有規律的排列，第2行最后一個數是4，第3行最后一個數是7，第4行最后一個數是10，…．按此規律，若2022是第m行第n個數，則m,n的值分別是（ ）