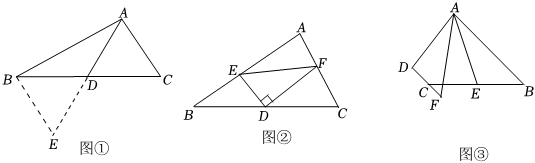
（1）方法呈現(xiàn)：如圖①：在△ABC中，若AB=6，AC=4，點(diǎn)D為BC邊的中點(diǎn)，求BC邊上的中線AD的取值范圍．
解決此問題可以用如下方法：
延長AD到點(diǎn)E，使DE=AD，再連接BE，可證△ACD≌△EBD，從而把AB、AC，2AD集中在△ABE中，利用三角形三邊的關(guān)系即可判斷中線AD的取值范圍是 1＜AD＜51＜AD＜5（直接寫出范圍即可）．這種解決問題的方法我們稱為“倍長中線法”；
（2）探究應(yīng)用：
如圖②，在△ABC中，點(diǎn)D是BC的中點(diǎn)，DE⊥DF于點(diǎn)D，DE交AB于點(diǎn)E，DF交AC于點(diǎn)F，連接EF，判斷BE+CF與EF的大小關(guān)系，并說明理由；
（3）問題拓展：
如圖③，在四邊形ABCD中，AB∥CD，AF與DC的延長線交于點(diǎn)F，點(diǎn)E是BC的中點(diǎn)，若AE是∠BAF的角平分線，試探究線段AB、AF、CF之間的數(shù)量關(guān)系，并說明理由．
【考點(diǎn)】三角形綜合題．
【答案】1＜AD＜5
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2033引用：3難度：0.1
相似題
-
1．綜合與實(shí)踐：
問題情境：數(shù)學(xué)活動(dòng)課上，王老師出示了一個(gè)問題：
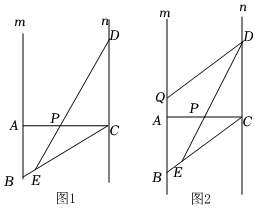
如圖1，直線m∥n,點(diǎn)A、B在直線m上（點(diǎn)B在點(diǎn)A的下方），過點(diǎn)A作AC⊥n于點(diǎn)C，連接BC，以C為圓心CA為半徑作弧，交直線n于點(diǎn)D，交BC于點(diǎn)E．求證：∠ABC=2∠CDE．
獨(dú)立思考：（1）請(qǐng)解答王老師提出的問題．
實(shí)踐探究：（2）DE與AC交于點(diǎn)P，在原有問題條件不變的情況下，王老師提出新問題，請(qǐng)你解答．
“猜想出AB、BC、PC的數(shù)量關(guān)系，并證明．”
問題解決：（3）過點(diǎn)D作DQ∥BC交m于點(diǎn)Q（點(diǎn)Q在點(diǎn)A上方），數(shù)學(xué)活動(dòng)小組同學(xué)對(duì)上述問題進(jìn)行特殊化研究之后發(fā)現(xiàn)，當(dāng)AQ=BE時(shí)，線段BE和AB有一定的數(shù)量關(guān)系，該小組提出下面的問題，請(qǐng)你解答．
“如圖2，當(dāng)AQ=BE時(shí)，求的值．”DPAB發(fā)布：2025/6/14 20:0:1組卷：171引用：2難度：0.1 -
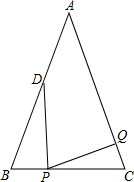2．如圖，已知△ABC中，AB=AC=6cm,∠B=∠C，BC=4cm,點(diǎn)D為AB的中點(diǎn)．
（1）如果點(diǎn)P在線段BC上以1cm/s的速度由點(diǎn)B向點(diǎn)C運(yùn)動(dòng)，同時(shí)，點(diǎn)Q在線段CA上由點(diǎn)C向點(diǎn)A運(yùn)動(dòng)．
①若點(diǎn)Q的運(yùn)動(dòng)速度與點(diǎn)P的運(yùn)動(dòng)速度相等，經(jīng)過1秒后，△BPD與△CPQ是否全等，請(qǐng)說明理由．
②若點(diǎn)Q的運(yùn)動(dòng)速度與點(diǎn)P的運(yùn)動(dòng)速度不相等，當(dāng)點(diǎn)Q的運(yùn)動(dòng)速度為 cm/s時(shí)，在某一時(shí)刻也能夠使△BPD與△CPQ全等．
（2）若點(diǎn)Q以②中的運(yùn)動(dòng)速度從點(diǎn)C出發(fā)，點(diǎn)P以原來的運(yùn)動(dòng)速度從點(diǎn)B同時(shí)出發(fā)，都按逆時(shí)針方向沿△ABC的三邊運(yùn)動(dòng)．求經(jīng)過多少秒后，點(diǎn)P與點(diǎn)Q第一次相遇，并寫出第一次相遇點(diǎn)在△ABC的哪條邊上？發(fā)布：2025/6/14 20:0:1組卷：112引用：2難度：0.3 -
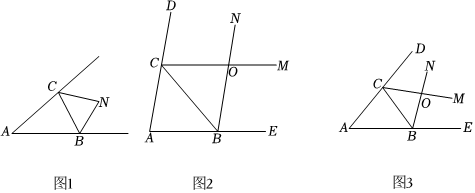
3．如圖1，在△ABC中，∠A=40°，外角平分線BN和CN相交于點(diǎn)N，求∠BNC的度數(shù)．
?
（1）請(qǐng)你先完成這個(gè)問題的解答．小明在完成以上問題的解答后，作如下變式探究：
（2）如圖2，在△ABC中，∠A=80°，若∠CBN=∠CBE，∠BCM=38∠BCD，BN與CM交于點(diǎn)O，求∠BOC的度數(shù)．38
（3）如圖3，在△ABC中，∠A=n°，若∠CBN=∠CBE，∠BCM=34∠BCD，當(dāng)射線CM與BN相交時(shí)，n的取值范圍是什么？試說明理由．34發(fā)布：2025/6/14 20:0:1組卷：257引用：2難度：0.4