2022-2023學年重慶市綦江區古南中學八年級（上）第一次定時作業數學試卷

一、選擇題（本大題共12小題，共48分。在每小題列出的選項中，選出符合題目的一項）

• 1．如圖，四個圖形中，線段BE是△ABC的高的圖是（　　）

  A．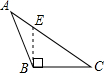

  B．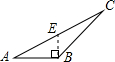

  C．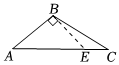

  D．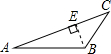
  組卷：9435引用：76難度：0.9

  解析

• 2．下列每組數分別表示三根木棒的長，將它們首尾連接后，能擺成三角形的一組是（　　）

  A．1，2，3

  B．1，2，4

  C．2，3，4

  D．2，2，4
  組卷：1556引用：30難度：0.9

  解析

• 3．在△ABC中，AB=BC，AB邊上的中線CD將△ABC的周長分為15和6兩個部分，求△ABC的三邊長分別為（　　）

  A．10，10，1

  B．4，4，13

  C．8，8，5

  D．9，9，3
  組卷：207引用：2難度：0.5

  解析

• 4．在△ABC中，∠A=

  1

  2

  ∠B=

  1

  3

  ∠C，則此三角形是（　　）

  A．銳角三角形

  B．直角三角形

  C．鈍角三角形

  D．等腰三角形
  組卷：4772引用：43難度：0.9

  解析

• 5．下列各組條件中，不能判定△ABC≌△A′B′C′的是（　　）

  A．AC=A′C′，BC=B′C′，∠C=∠C′

  B．∠A=∠A′，BC=B′C′，AC=A′C′

  C．AC=A′C′，AB=A′B′，∠A=∠A′

  D．AC=A′C′，∠A=∠A′，∠C=∠C′
  組卷：71引用：4難度：0.9

  解析

• 6．若從一多邊形的一個頂點出發，最多可引10條對角線，則它是（　　）

  A．十三邊形

  B．十二邊形

  C．十一邊形

  D．十邊形
  組卷：2267引用：49難度：0.9

  解析

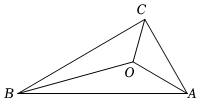• 7．如圖，△ABC的三邊AC、BC、AB的長分別是8、12、16，點O是△ABC三條角平分線的交點，則S_△OAB：S_△OBC：S_△OAC的值為（　　）

  A．4：3：2

  B．1：2：3

  C．2：3：4

  D．3：4：5
  組卷：2105引用：15難度：0.7

  解析

• 8．如圖，若∠A=70°，∠B=40°，∠C=32°．則∠BDC=（　　）

  A．102°

  B．110°

  C．142°

  D．148°
  組卷：816引用：10難度：0.7

  解析

四、解答題（本大題共7小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

• 24．對一個任意三位數M=a

  b

  c,如果M滿足各個數位上的數字互不相同，且都不為零，現將M各個數位上的數字從左往右由大到小排列得到一個新數M₁，將M各個數位上的數字從左往右由小到大排列得到一個新數M₂，記F（M）=

  M

  1

  +

  M

  2

  7

  ，如果F（M）為整數，則稱M為“7倍和數”．
  例如：M=326，則F（326）=

  632

  +

  236

  7

  =124是整數，所以326是“7倍和數”；M=123，則F（123）=

  321

  +

  123

  7

  =63

  3

  7

  不是整數，所以123不是“7倍和數”．
  （1）判斷324，745是否是“7倍和數”，并說明理由；
  （2）T=100a+90+b（1≤a＜b＜9），a,b都是正整數，T是“7倍和數”，求T的值．
  組卷：43引用：1難度：0.5

  解析

• 25．（1）方法呈現：如圖①：在△ABC中，若AB=6，AC=4，點D為BC邊的中點，求BC邊上的中線AD的取值范圍．
  解決此問題可以用如下方法：
  延長AD到點E，使DE=AD，再連接BE，可證△ACD≌△EBD，從而把AB、AC，2AD集中在△ABE中，利用三角形三邊的關系即可判斷中線AD的取值范圍是

  （直接寫出范圍即可）．這種解決問題的方法我們稱為“倍長中線法”；
  （2）探究應用：
  如圖②，在△ABC中，點D是BC的中點，DE⊥DF于點D，DE交AB于點E，DF交AC于點F，連接EF，判斷BE+CF與EF的大小關系，并說明理由；
  （3）問題拓展：
  如圖③，在四邊形ABCD中，AB∥CD，AF與DC的延長線交于點F，點E是BC的中點，若AE是∠BAF的角平分線，試探究線段AB、AF、CF之間的數量關系，并說明理由．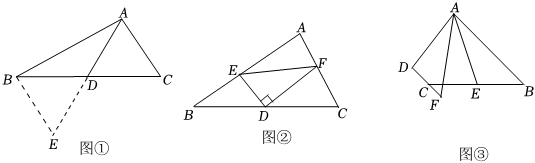
  
  組卷：2027引用：3難度：0.1

  解析