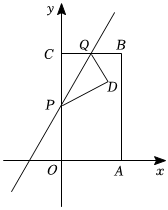
如圖，矩形OABC的頂點A，C分別在x軸和y軸上，OA，OC（OA＜OC）的長是一元二次方程x2-（3+33）x+93=0的兩個實數根，點P從點C出發，以每秒3個單位長度的速度向終點O運動，同時點Q從點C出發，以每秒1個單位長度的速度向終點B運動，將△CPQ沿直線PQ折疊得到△DPQ，設△DPQ與矩形OABC重合部分的面積為S，運動時間為t秒．
（1）求點B的坐標；
（2）求S與t的函數關系式，并寫出自變量的取值范圍；
（3）當點D落在AB上時，點N在x軸上，直線PQ上是否存在點M，使以D，Q，M，N為頂點的四邊形是平行四邊形？若存在，直接出點M的坐標；若不存在，請說明理由．
x
2
-
（
3
+
3
3
）
x
+
9
3
=
0
3
【考點】四邊形綜合題．
【答案】（1）；
（2）
；
（3）或或．
（
3
，
3
3
）
（2）
S
=
3 2 t 2 ， 0 ＜ t ≤ 2 |
- 3 t 2 + 6 3 t - 6 3 ， 2 ＜ t ≤ 3 |
（3）
（
0
，
3
）
（
-
2
，-
3
）
（
4
，
5
3
）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/8 8:0:8組卷：45引用：3難度：0.3
相似題
-
1．綜合與實踐
問題情境：在綜合實踐課上，老師讓大家動手操作三角形紙片的折疊問題，“智慧”小組提供了如下折疊方法：
（1）如圖①，經過點A的直線折疊△ABC紙片，使得邊AB落在AC邊上，折痕為AM，AM交BC于點D，得到圖②，再將紙片展平在一個平面上，得到圖③．
（2）再次折疊△ABC紙使得A與點D重合，折痕為PQ，得到圖④，再次將紙片展平在一個平面上，連接DP，DQ，得到圖⑤．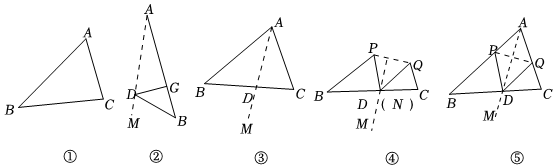
操作與發現：（1）證明四邊形APDQ是菱形．
操作與探究：（2）在圖⑤中，若∠B+∠C=120°，AD=6，求PD的長．
操作與實踐：（3）若△ABC中，∠BAC=90°，AB=4，AC=3，通過從圖①一圖⑤的折疊，那么最后折疊成的四邊形APDQ的面積為 ．（直接寫出即可）發布：2025/5/25 23:0:2組卷：284引用：5難度：0.3 -
2．【閱讀理解】人教版七年級下冊8.3探究2：據統計資料，甲、乙兩種作物的單位面積產值的比是1：2，現要把一塊長AB為200m、寬AD為100m的長方形土地分為兩塊土地，分別種植這兩種作物，怎么樣劃分這塊土地，使甲、乙兩種作物的總產量的比是3：4？
【解題過程】如圖1，若甲、乙兩種作物的種植區分別為長方形AMND和MNCB，此時設AM=xm,MB=ym,根據題意，列出方程組：，解得100x：2×100y=3：4x+y=200．x=120y=80
過長方形土地的長邊上離一端120m處，作這條邊的垂線，把這塊土地分為兩塊長方形土地，較大一塊土地種植甲作物，其面積為：100×120=12000m2，
較小的一塊土地種乙種作物，其面積為：80×100=8000m2．
【嘗試應用】同學們從以上解決方法得到啟發提出解決上述問題的另一思路：
若按如圖2所示，劃分出一塊三角形土地AMN種植乙種作物，其余土地種植甲種作物，則AM應該取多長？
【拓展應用】現要把另一塊長AB為200m、寬AD為100m的長方形土地建成花園小廣場，設計方案如圖3所示，陰影區域為綠化區（四塊綠化區為全等的直角三角形），空白區域為活動區，且四周出口寬度一樣（EF=GH=MN=PQ），設EF=xm（55≤x≤60）．當出口寬為多少米時，活動區的面積最大？最大面積是多少？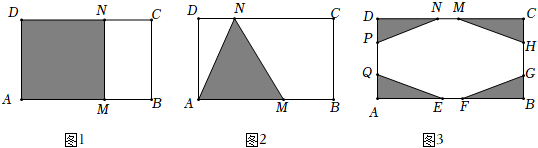
發布：2025/5/25 23:0:2組卷：197引用：1難度：0.4 -
3．【問題情境】
如圖1，在等腰直角三角形ABC中，∠ACB=90°，F是AC邊上一動點（點F不與點A，C重合），以CF為邊在△ABC外作正方形CDEF，連接AD，BF．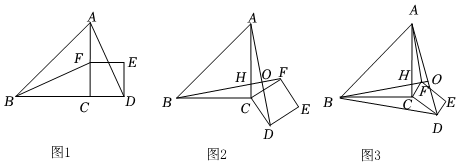
【探究展示】
（1）①猜想：圖1中，線段BF，AD的數量關系是 ，位置關系是 ．
②如圖2，將圖1中的正方形CDEF繞點C順時針旋轉α，BF交AC于點H，交AD于點O，①中的結論是否仍然成立？請說明理由．
【拓展延伸】
（2）如圖3，將【問題情境】中的等腰直角三角形ABC改為直角三角形ABC，∠ACB=90°，正方形CDEF改為矩形CDEF，連接BF并延長，交AC于點H，交AD于點O，連接BD，AF．若AC=4，BC=3，CD=，CF=1，求BD2+AF2的值．43發布：2025/5/25 23:30:1組卷：246引用：3難度：0.4