已知△ABC中，如果過頂點B的一條直線把這個三角形分割成兩個三角形，其中一個為等腰三角形，另一個為直角三角形，則稱這條直線為△ABC的關于點B的二分割線．例如：如圖1，Rt△ABC中∠A=90°，∠C=20°，若過頂點B的一條直線BD交AC于點D，若∠DBC=20°，顯然直線BD是△ABC的關于點B的二分割線．
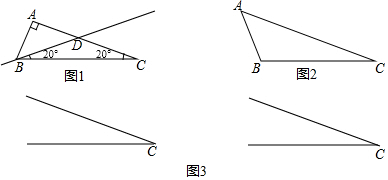
（1）在圖2的△ABC中，∠C=20°，∠ABC=110°，請在圖2中畫出△ABC關于點B的二分割線，且∠DBC角度是20°20°．
（2）已知∠C=20°，在圖3中畫出不同于圖1，圖2的△ABC，所畫△ABC同時滿足：
①∠C為最小角；
②存在關于點B的二分割線，∠BAC的度數是35°或45°35°或45°．
（3）已知∠C=a,△ABC同時滿足：
①∠C為最小角；
②存在關于點B的二分割線，請求出∠BAC的度數（用a表示）．
【考點】三角形綜合題．
【答案】20°；35°或45°
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/7/17 8:0:9組卷：583引用：5難度：0.3
相似題
-
1．如圖，△ABC中，∠BAC=90°，以直角邊AC為腰，向外作等腰直角三角形ACD，AC=CD，∠ACD=90°，點E是BC邊上一點，且CE=CD，∠ABC=2∠CED．
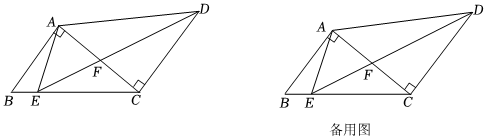
（1）探究：∠CDE與∠ACB的數量關系；
（2）求證：BC=CF+AB；
（3）若AD=4，AB=3，求EF的長．2發(fā)布：2025/6/5 12:0:1組卷：417引用：5難度：0.1 -
2．已知：如圖1，線段AB=14cm,△PAB的頂點P從點A出發(fā)沿折線A-O-B運動時，△PAB的面積隨著點P運動路程的變化，發(fā)生了變化．圖2表示這種變化規(guī)律．
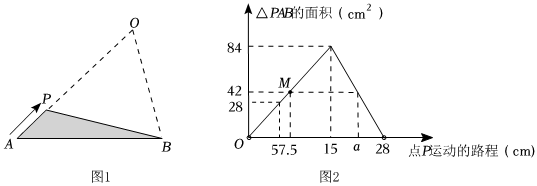
（1）在P點運動5cm時，△PAB的面積為 cm2；當P點運動路程為 cm時，△PAB的面積最大為 cm2；
（2）求圖1中線段AO、OB的長，以及O到AB的距離；
（3）直接寫出a的值為 ．發(fā)布：2025/6/5 11:30:2組卷：22引用：2難度：0.3 -
3．如圖，點C為線段AE上一動點（不與點A、E重合），在AE同側分別作等邊△ABC和等邊△CDE，AD與BE交于點O，AD與BC交于點P，BE與CD交于點Q，連接PQ，以下結論：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤線段AD繞著點C順時針旋轉60度可與線段BE重合；⑥△CPQ為等邊三角形；正確的有 ．（填序號）發(fā)布：2025/6/5 11:30:2組卷：306引用：1難度：0.3