定義：對于一個四邊形，我們把依次連接它的各邊中點得到的新四邊形叫做原四邊形的“中點四邊形”．如果原四邊形的中點四邊形是個正方形，我們把這個原四邊形叫做“中方四邊形”．
【概念理解】
（1）在已經學過的“①平行四邊形：②矩形：③菱形：④正方形”中，④④的“中點四邊形”一定是正方形，因此它一定是“中方四邊形”（填序號）．
【性質探究】
（2）如圖1，若四邊形ABCD是“中方四邊形”，觀察圖形，寫出關于四邊形ABCD的一條結論：AC⊥BD，AC=BDAC⊥BD，AC=BD．
【問題解決】
（3）如圖2，以銳角△ABC的兩邊AB，AC為邊長，分別向外側作正方形ABDE和正方形ACFG，連結BE，EG，GC，依次連接四邊形BCGE的四邊中點得到四邊形MNRL．求證：四邊形BCGE是“中方四邊形”．
【考點】四邊形綜合題．
【答案】④；AC⊥BD，AC=BD
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 4:0:3組卷：188引用：1難度：0.2
相似題
-
1．（1）問題背景：如圖①，在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分別是BC，CD上的點，且∠EAF=60°，請探究圖中線段BE，EF，DF之間的數量關系，小明同學探究此問題的方法是：延長FD到點G，使DG=BE．連接AG，先證明△ABE≌△ADG，得AE=AG；再由條件可得∠EAF=∠GAF，證明△AEF≌△AGF，進而可得線段BE，EF，DF之間的數量關系是 ．
（2）探索延伸：如圖②，在四邊形ABCD中，AB=AD，∠B+∠D=180°．E，F分別是BC，CD上的點，且∠EAF=∠BAD．問（1）中的線段BE，EF，DF之間的數量關系是否還成立？若成立，請給出證明；若不成立，請說明理由．12
（3）實際應用：如圖③，在某次軍事演習中，艦艇甲在指揮中心（O處）北偏西20°的A處，艦艇乙在指揮中心南偏東80°的B處，并且兩艦艇到指揮中心的距離相等，接到行動指令后，艦艇甲向正東方向以50海里/小時的速度前進，艦艇乙沿北偏東30°的方向以60海里/小時的速度前進．2小時后，甲、乙兩艦艇分別到達E，F處，此時在指揮中心觀測到兩艦艇之間的夾角為60°，試求此時兩艦艇之間的距離．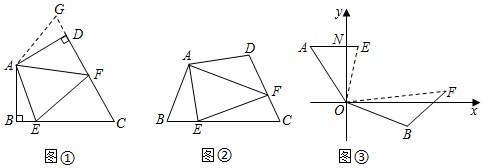
發布：2025/6/2 21:0:1組卷：278引用：3難度：0.1 -
2．如圖1所示，邊長為4的正方形ABCD與邊長為a（0＜a＜4）的正方形CFEG的頂點C重合，點E在對角線AC上．
（1）【問題發現】如圖1所示，AE與BF的數量關系為 ；
（2）【類比探究】如圖2所示，將正方形CFEG繞點C旋轉，旋轉角為α（0＜α＜30°），請問此時上述結論是否還成立？若成立，寫出推理過程，若不成立，說明理由；
（3）【拓展延伸】當時，正方形CFEG若按圖1所示位置開始旋轉，在正方形CFEG的旋轉過程中，當點A、F、C在一條直線上時，請直接寫出此時線段AE的長 ．a=2發布：2025/6/2 21:30:9組卷：370引用：2難度：0.1 -
3．問題背景
定義：若兩個等腰三角形有公共底邊，且兩個頂角的和是180°，則稱這兩個三角形是關于這條底邊的互補三角形．如圖1，四邊形ABCD中，BC是一條對角線，AB=AC，DB=DC，且∠A+∠D=180°，則△ABC與△DBC是關于BC的互補三角形．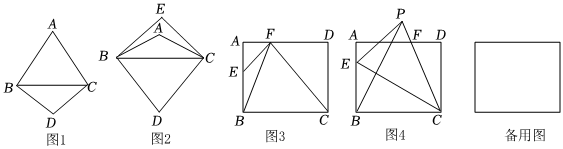
（1）初步思考：如圖2，在△ABC中，AB=AC，∠ABC=30°，D、E為△ABC外兩點，EB=EC，∠EBC=45°，△DBC為等邊三角形．則△ABC關于BC的互補三角形是 ，并說明理由．
（2）實踐應用：如圖3，在長方形ABCD中，AB=8，AD=10．點E在AB邊上，點F在AD邊上，若△BEF與△BCF是關于BF互補三角形，試求AE的長．
（3）思維探究：如圖4，在長方形ABCD中，AB=8，AD=10．點E是線段AB上的動點，點P是平面內一點，△BEP與△BCP是關于BP的互補三角形，直線CP與直線AD交于點F．在點E運動過程中，線段BE與線段AF的長度是否會相等？若相等，請直接寫出AE的長；若不相等，請說明理由．發布：2025/6/2 17:30:1組卷：304引用：5難度：0.3