在七年級的學習中,我們知道:(1)三角形的內角和等于180°,
(2)等腰三角形的兩個底角相等.下面我們對這兩點知識作進一步思考和探索.
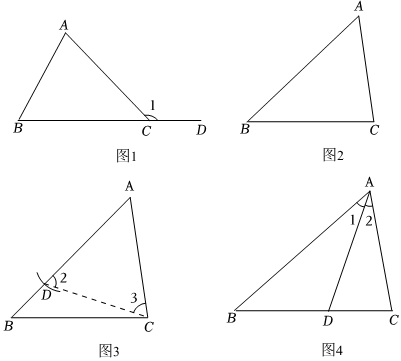
(一)三角形的外角.三角形內角的一條邊與另一條邊的反向延長線組成的角,稱為三角形的外角.如圖1,∠1就是△ABC的∠ACB的外角.在三角形的每個頂點位置都可以找到它的外角,以∠1為例,我們探索外角與其它角的關系.
∵∠1+∠ACB=180°(①平角的定義平角的定義),
∠A+∠B+∠ACB=180°(②三角形的內角和定理三角形的內角和定理),
∴∠1=180°-∠ACB,∠A+∠B=180°-∠ACB,
∴∠1=∠A+∠B(③等量代換等量代換),
∴∠1>∠A,∠1>∠B,
由此我們得到了三角形外角的兩條性質:
(1)三角形的一個外角等于和它不相鄰的兩個內角的和;
(2)三角形的一個外角大于任何一個和它不相鄰內角;
問題1:(1)請在以上括號①②③中填上適當的理由;
(2)請在圖1中分別畫出∠BAC和∠ABC的一個外角,并分別標注為∠2,∠3;
(二)等腰三角形的兩個底角相等.等腰三角形的兩個底角相等,我們簡述為“等邊對等角”,數學小組據此提出問題:三角形中大邊對的內角也大,即“大邊對大角”正確嗎?小聰同學進行了如下探索.
問題2:如圖2,△ABC中AB>AC,求證:∠ACB>∠B,證明:如圖3,在AB邊上截取AD=AC,連接CD,
∵AD=AC,
∴∠2=∠3(④等邊對等角等邊對等角),
∵∠ACB>∠3(整體大于部分),
又∵∠2>∠B(⑤三角形的外角大于任意一個與其不相鄰的內角三角形的外角大于任意一個與其不相鄰的內角),
∴∠ACB>∠B,
由此說明三角形中大邊對大角,請在以上括號④⑤中填上適當的理由.
問題3:如圖4,△ABC中∠1=∠2,AB=AC+CD,請判斷∠C=2∠B是否成立,并說明理由.
【考點】三角形綜合題.
【答案】平角的定義;三角形的內角和定理;等量代換;等邊對等角;三角形的外角大于任意一個與其不相鄰的內角
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/4 8:0:5組卷:366引用:1難度:0.4
相似題
-
1.已知AB=BC,∠ABC=90°,直線l是過點B的一條動直線(不與直線AB,BC重合),分別過點A,C作直線l的垂線,垂足為D,E.
(1)如圖1,當45°<∠ABD<90°時,
①求證:CE+DE=AD;
②連接AE,過點D作DH⊥AE于H,過點A作AF∥BC交DH的延長線于點F.依題意補全圖形,用等式表示線段DF,BE,DE的數量關系,并證明;
(2)在直線l運動的過程中,若DE的最大值為3,直接寫出AB的長.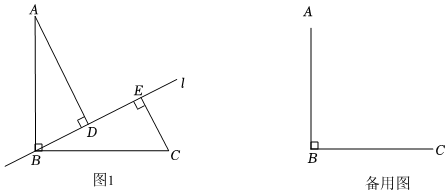 發布:2025/5/23 20:30:1組卷:1374引用:5難度:0.4
發布:2025/5/23 20:30:1組卷:1374引用:5難度:0.4 -
2.課本再現
如圖1,在等邊△ABC中,E為邊AC上一點,D為BC上一點,且AE=CD,連接AD與BE相交于點F.
(1)AD與BE的數量關系是 ,AD與BE構成的銳角夾角∠BFD的度數是 ;
深入探究
(2)將圖1中的AD延長至點G,使FG=BF,連接BG,CG,如圖2所示.求證:GA平分∠BGC.(第一問的結論,本問可直接使用)
遷移應用
(3)如圖3,在等腰△ABC中,AB=AC,D,E分別是邊BC,AC上的點,AD與BE相交于點F.若∠BAC=∠BFD,且BF=3AF,求值.BDCD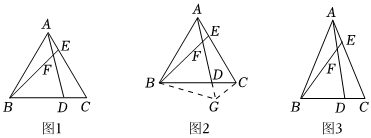 發布:2025/5/23 20:30:1組卷:1077引用:3難度:0.1
發布:2025/5/23 20:30:1組卷:1077引用:3難度:0.1 -
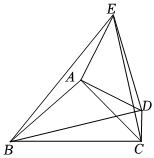 3.如圖,在△ABC中,AB=AC=3,∠BAC=90°,點D為一個動點,且點D到點C的距離為1,連接CD,AD,作EA⊥AD,使AE=AD.
3.如圖,在△ABC中,AB=AC=3,∠BAC=90°,點D為一個動點,且點D到點C的距離為1,連接CD,AD,作EA⊥AD,使AE=AD.
(1)求證:△ADB≌△AEC;
(2)求證:BD⊥EC;
(3)直接寫出BD最大和最小值;
(4)點D在直線AC上時,求BD的長.發布:2025/5/23 21:0:1組卷:103引用:2難度:0.4


