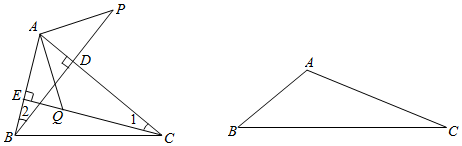
如圖所示，BD、CE是△ABC的高，點P在BD的延長線上，CA=BP，點Q在CE上，QC=AB．
（1）探究PA與AQ之間的關(guān)系；
（2）若把（1）中的△ABC改為鈍角三角形，AC＞AB，∠A是鈍角，其他條件不變，上述結(jié)論是否成立？畫出圖形并證明你的結(jié)論．
【考點】全等三角形的判定與性質(zhì)．
【答案】（1）AP=AQ，AP⊥AQ；
（2）成立．
（2）成立．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2872引用：9難度：0.3
相似題
-
1．在Rt△ABC中，∠BAC=90°，AC=AB，點F是射線CA上一點，連接BF，過點C作CE⊥BF，垂足為點E，直線CE、AB相交于點D．
（1）如圖1所示，當(dāng)點F在線段CA延長線上時，求證：△CAD≌△BAF；
（2）如圖2所示，當(dāng)點F在線段CA上時，連接EA，過點A作AM⊥BE于M，AN⊥CE于N，求證：EA平分∠DEB．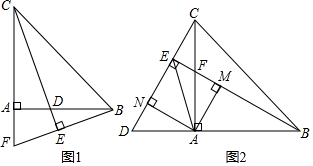
發(fā)布：2025/5/22 14:30:2組卷：78引用：3難度：0.7 -
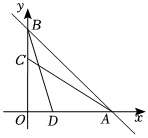2．平面直角坐標(biāo)系中，O為坐標(biāo)原點，直線y=-x+4與x軸、y軸分別交于A，B兩點，點C，點D坐標(biāo)分別為（0，m），（4-m,0）（0＜m＜4），則AC+BD的最小值為 ．發(fā)布：2025/5/22 14:30:2組卷：389引用：4難度：0.6 -
3．在證明“等腰三角形的兩個底角相等”這個性質(zhì)定理時，添加的輔助線AD有以下兩種不同的敘述方法，請選擇其中一種完成證明．
等腰三角形的性質(zhì)定理：等腰三角形的兩個底角相等
已知：如圖，在△ABC中，AB=AC．求證：∠B=∠C．法一
證明：如圖，作∠BAC的平分線交BC于點D．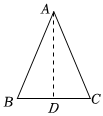
法二
證明：如圖，取BC的中點D，連接AD．發(fā)布：2025/5/22 15:30:1組卷：175引用：2難度：0.5