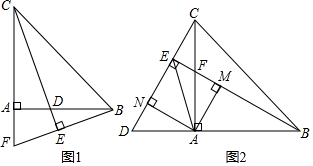
在Rt△ABC中，∠BAC=90°，AC=AB，點(diǎn)F是射線CA上一點(diǎn)，連接BF，過點(diǎn)C作CE⊥BF，垂足為點(diǎn)E，直線CE、AB相交于點(diǎn)D．
（1）如圖1所示，當(dāng)點(diǎn)F在線段CA延長線上時，求證：△CAD≌△BAF；
（2）如圖2所示，當(dāng)點(diǎn)F在線段CA上時，連接EA，過點(diǎn)A作AM⊥BE于M，AN⊥CE于N，求證：EA平分∠DEB．

【答案】（1）見解析；
（2）見解析．

【解答】

【點(diǎn)評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/5/22 14:30:2組卷：78引用：3難度：0.7

相似題

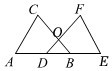1．如圖，點(diǎn)A，D，B，E在同一條直線上，BC與DF相交于點(diǎn)O，AC=EF，AD=BE，BC=DF，求證：OD=OB．
發(fā)布：2025/5/22 17:0:1組卷：225引用：1難度：0.6
解析

2．在證明“等腰三角形的兩個底角相等”這個性質(zhì)定理時，添加的輔助線AD有以下兩種不同的敘述方法，請選擇其中一種完成證明．

等腰三角形的性質(zhì)定理：等腰三角形的兩個底角相等
已知：如圖，在△ABC中，AB=AC．求證：∠B=∠C．

法一
證明：如圖，作∠BAC的平分線交BC于點(diǎn)D．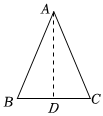
法二
證明：如圖，取BC的中點(diǎn)D，連接AD．

發(fā)布：2025/5/22 15:30:1組卷：175引用：2難度：0.5

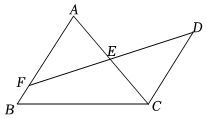3．已知：如圖，在△ABC中，E是AC的中點(diǎn)，點(diǎn)F在AB上，CD∥AB，交FE的延長線于點(diǎn)D．
（1）求證：EF=ED；
（2）若AB=8，CD=6，求BF的長．
發(fā)布：2025/5/22 18:0:2組卷：687引用：4難度：0.5
解析

相關(guān)試卷

等腰三角形的性質(zhì)定理：等腰三角形的兩個底角相等已知：如圖，在△ABC中，AB=AC．求證：∠B=∠C．
法一證明：如圖，作∠BAC的平分線交BC于點(diǎn)D．	法二證明：如圖，取BC的中點(diǎn)D，連接AD．