分類討論是重要的數(shù)學(xué)方法，如化簡(jiǎn)|x|，當(dāng)x＞0時(shí)，|x|=x；當(dāng)x=0時(shí)，|x|=0；當(dāng)x＜0時(shí)，|x|=-x.求解下列問題：
（1）當(dāng)x=-3時(shí)，x|x|值為 -1-1，當(dāng)x=3時(shí)，x|x|的值為 11，當(dāng)x為不等于0的有理數(shù)時(shí)，x|x|的值為 ±1±1；
（2）已知x+y+z=0，xyz＞0，求y+z|x|+x+z|y|-x+y|z|的值；
（3）已知：x1，x2，…，x2021，x2022，x2023，這2023個(gè)數(shù)都是不等于0的有理數(shù)，若這2023個(gè)數(shù)中有n個(gè)正數(shù)，m=x1|x1|+x2|x2|+…+x2021|x2021|+x2022|x2022|+x2023|x2023|，則m的值為 2n-20232n-2023（請(qǐng)用含n的式子表示）．
x
|
x
|
x
|
x
|
x
|
x
|
y
+
z
|
x
|
+
x
+
z
|
y
|
-
x
+
y
|
z
|
m
=
x
1
|
x
1
|
+
x
2
|
x
2
|
+
…
+
x
2021
|
x
2021
|
+
x
2022
|
x
2022
|
+
x
2023
|
x
2023
|
【答案】-1；1；±1；2n-2023
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/31 9:30:2組卷：930引用：5難度：0.3
相似題
-
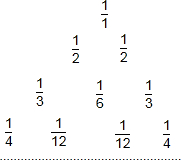1．如圖所示的數(shù)碼叫“萊布尼茨調(diào)和三角形”，它們是由整數(shù)的倒數(shù)組成的，第n行有n個(gè)數(shù)，且兩端的數(shù)均為，每個(gè)數(shù)是它下一行左右相鄰兩數(shù)的和，則第8行第3個(gè)數(shù)（從左往右數(shù)）為（ ）1n發(fā)布：2025/6/1 21:0:1組卷：3757引用：79難度：0.3 -
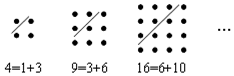2．古希臘著名的畢達(dá)哥拉斯學(xué)派把1、3、6、10 …這樣的數(shù)稱為“三角形數(shù)”，而把1、4、9、16…這樣的數(shù)稱為“正方形數(shù)”．從圖中可以發(fā)現(xiàn)，任何一個(gè)大于1的“正方形數(shù)”都可以看作兩個(gè)相鄰“三角形數(shù)”之和．則下列符合這一規(guī)律的等式是（ ）發(fā)布：2025/6/1 20:0:1組卷：399引用：3難度：0.7 -
=
3．閱讀下列材料：
因?yàn)?div id="ouea0eg" class="MathJye" mathtag="math">11×3×（1-12），13=13×5×（12-13），15=15×7×（12-15），…，17=12019×2021×12-12019，所以12021+11×3+13×5+…+15×7=12019×2021×（1-12-13+13+15-15+17+?+17-12019）=12021×（1-12）=12021．10102021
解答下列問題：
（1）在和式+11×3+13×5+…中，第5項(xiàng)為 ，第n項(xiàng)為 ，上述求和的思想方法是通過逆用異分母分?jǐn)?shù)減法法則，將和式中的各分?jǐn)?shù)轉(zhuǎn)化為兩個(gè)數(shù)的差，使得首末兩項(xiàng)外的中間各項(xiàng)可以 ，從而達(dá)到求和的目的；15×7
（2）利用上述結(jié)論計(jì)算：+1x（x+2）+1（x+2）（x+4）+…+1（x+4）（x+6）．1（x+2020）（x+2022）
發(fā)布：2025/6/1 21:0:1組卷：161引用：1難度：0.5