當(dāng)前位置：
試題詳情
關(guān)于橢圓的切線有下列結(jié)論：若P（x1，y1）是橢圓x2a2+y2b2=1（a＞b＞0）上的一點(diǎn)，則過點(diǎn)P的橢圓的切線方程為x1xa2+y1yb2=1．已知橢圓C：x24+y23=1，過橢圓C外一點(diǎn)M（x0，y0）作橢圓的兩條切線MA，MB（A，B為切點(diǎn)）．
（Ⅰ）利用上述結(jié)論，求過橢圓C上的點(diǎn)P（1，n）（n＞0）的切線方程；
（Ⅱ）若M是直線x=4上的任一點(diǎn)，過M作橢圓C的兩條切線MA，MB（A，B為切點(diǎn)），設(shè)橢圓的右焦點(diǎn)為F，求證：MF⊥AB．
x
2
a
2
+
y
2
b
2
=
1
x
1
x
a
2
+
y
1
y
b
2
=
1
x
2
4
+
y
2
3
=
1
【考點(diǎn)】橢圓的切線方程及性質(zhì)．
【答案】（Ⅰ）x+2y-4=0；
（Ⅱ）證明：設(shè)M（4，t），A（x1，y1），B（x2，y2），
則過A，B兩點(diǎn)的橢圓C的切線MA，MB的方程為：
，．
∵M(jìn)（4，t）在兩切線上，∴，．
∴A，B兩點(diǎn)均在直線上，即直線AB的方程為x+．
當(dāng)t≠0時，，
又F（1，0），∴，，
∴MF⊥AB；
若t=0，點(diǎn)M（4，0）在x軸上，A，B兩點(diǎn)關(guān)于x軸對稱，顯然MF⊥AB．
軸上，MF⊥AB．
（Ⅱ）證明：設(shè)M（4，t），A（x1，y1），B（x2，y2），
則過A，B兩點(diǎn)的橢圓C的切線MA，MB的方程為：
x
1
x
4
+
y
1
y
3
=
1
x
2
x
4
+
y
2
y
3
=
1
∵M(jìn)（4，t）在兩切線上，∴
4
x
1
4
+
t
y
1
3
=
1
4
x
2
4
+
t
y
2
3
=
1
∴A，B兩點(diǎn)均在直線
4
x
4
+
ty
3
=
1
ty
3
=
1
當(dāng)t≠0時，
k
AB
=
-
3
t
又F（1，0），∴
k
MF
=
t
-
0
4
-
1
=
t
3
k
AB
?
k
MF
=
-
3
t
?
t
3
=
-
1
∴MF⊥AB；
若t=0，點(diǎn)M（4，0）在x軸上，A，B兩點(diǎn)關(guān)于x軸對稱，顯然MF⊥AB．
軸上，MF⊥AB．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/11/7 8:0:2組卷：136引用：2難度：0.4
相似題
-
1．已知橢圓C的兩個頂點(diǎn)分別為A（-2，0），B（2，0），焦點(diǎn)在x軸上，離心率為．32
（Ⅰ）求橢圓C的方程；
（Ⅱ）已知點(diǎn)P（x0，y0）是橢圓上一點(diǎn)，求以點(diǎn)P為切點(diǎn)的橢圓的切線方程；
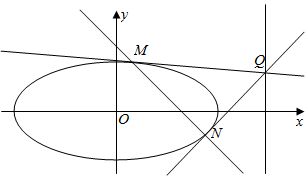
（Ⅲ）設(shè)點(diǎn)Q是直線l：x=5上一動點(diǎn)，過點(diǎn)Q作橢圓C的兩條切線QM，QN，切點(diǎn)分別為M，N，直線MN是否過定點(diǎn)？如果是，請求出定點(diǎn)坐標(biāo)；如果不是，請說明理由．發(fā)布：2024/11/7 8:0:2組卷：147引用：1難度：0.4 -
2．經(jīng)研究發(fā)現(xiàn)，若點(diǎn)M（x0，y0）在橢圓
上，則過點(diǎn)M的橢圓切線方程為x2a2+y2b2=1（a＞b＞0），現(xiàn)過點(diǎn)x0xa2+y0yb2=1作橢圓P（t,0）（|t|＞2）的切線，切點(diǎn)為Q，當(dāng)△POQ（其中O為坐標(biāo)原點(diǎn)）的面積為C：x22+y2=1時，t=．12發(fā)布：2024/11/7 8:0:2組卷：58引用：1難度：0.5 -
3．關(guān)于橢圓的切線有下列結(jié)論：若P（x1，y1）是橢圓
+x2a2=1（a＞b＞0）上的一點(diǎn)，則過點(diǎn)P的橢圓的切線方程為y2b2．已知橢圓C：x1xa2+y1yb2=1，過橢圓C外一點(diǎn)M（x0，y0）作橢圓的兩條切線MA，MB（A，B為切點(diǎn)）．x24+y23=1
（Ⅰ）利用上述結(jié)論，求直線AB的方程；
（Ⅱ）設(shè)橢圓的右焦點(diǎn)為F，求證：．|MF|2|FA||FB|=x204+y203發(fā)布：2024/11/7 8:0:2組卷：251引用：1難度：0.3