如圖，在矩形ABCD中，AB=6，BC=23，連接AC．點P從點A出發，沿折線A→B→C向終點C運動，在AB上的速度為每秒2個單位長度，在BC上的速度為每秒3個單位長度；過點P作PF⊥AC于點E，交線段AD或DC于點F，連接AP，AF．設點P運動的時間為x秒，△APF與△ADC重合部分的圖形面積為y.
（1）當點P在AB上時，用含x的式子表示AE的長，并寫出x的取值范圍．
（2）求y關于x的函數解析式，并寫出x的取值范圍．
（3）當點E為PF的三等分點時，直接寫出x的值．
BC
=
2
3
3
【考點】四邊形綜合題．
【答案】（1）；
（2）
；
（3）或．
AE
=
3
x
（
0
＜
x
≤
3
）
（2）
y =
| ||||||
（3）
4
3
8
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：91引用：2難度：0.3
相似題
-
1．在數學興趣社團課上，同學們對平行四邊形進行了深入探究．
探究一：如圖1，在矩形ABCD中，AC2=AB2+BC2，BD2=AC2=CD2+AD2，則AC2+BD2=AB2+BC2+CD2+AD2，由此得出結論：矩形兩條對角線的平方和等于其四邊的平方和．
探究二：對于一般的平行四邊形，是否仍有上面的結論呢？
證明：如圖2，在?ABCD中，過A作AM⊥BC于M，過D作DN⊥BC，交BC延長線于N．設AB=a,BC=b,BM=x,AM=y,
∵四邊形ABCD是平行四邊形，∴AB∥CD，AB=CD，∴∠ABC=∠DCN，
又∵∠AMB=∠DNC=90°，∴△ABM≌△DCN．
∴CN=BM=x,DN=AM=y.
請你接著完成上面的證明過程．
結論應用：若一平行四邊形的周長為20，兩條對角線長分別為8，2，求該平行四邊形的四條邊長．10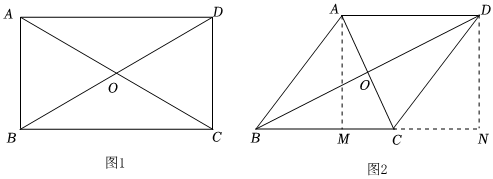
發布：2025/5/22 18:30:2組卷：223引用：1難度：0.5 -
2．如圖，在△ABC中，O是AB的中點，過A作BC的平行線，交CO延長線于D，點E，F分別是BC，AD的中點，連接AE和BF．
（1）求證：△OBC≌△OAD；
（2）請從以下兩個問題中選擇其中一個進行解答，（若多選，按第一個解答計分）
①當△ABC滿足什么條件時，四邊形AEBF是菱形？請加以證明；
②當△ABC滿足什么條件時，四邊形AEBF是矩形？請加以證明．
發布：2025/5/22 19:30:1組卷：182引用：1難度：0.5 -
3．（1）【證明體驗】如圖1，正方形ABCD中，E、F分別是邊AB和對角線AC上的點，∠EDF=45°．
①求證：△DBE～△DCF；
②=；BECF
（2）【思考探究】如圖2，矩形ABCD中，AB=6，BC=8，E、F分別是邊AB和對角線AC上的點，tan∠EDF=，BE=5，求CF的長；43
（3）【拓展延伸】如圖3，菱形ABCD中，BC=5，對角線AC=6，BH⊥AD交DA的延長線于點H，E、F分別是線段HB和AC上的點，tan∠EDF=，HE=34，求CF的長．85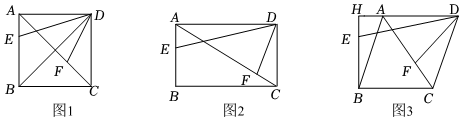
發布：2025/5/22 19:30:1組卷：1727引用：13難度：0.2
相關試卷