已知函數(shù)y1=-x2+（m+2）x-2m+1和函數(shù)y2=（n+2）x-2n-3，其中，m,n為常數(shù)，且n≠-2，記函數(shù)y1的頂點(diǎn)為P．
（1）當(dāng)m=0時(shí)，點(diǎn)P恰好在函數(shù)y2的圖象上，求n的值；
（2）隨著m的變化，點(diǎn)P是否都在某一條拋物線(xiàn)上？如果是，求出該拋物線(xiàn)的解析式，如果不是，請(qǐng)說(shuō)明理由；
（3）當(dāng)-1＜x＜2時(shí)，總有y2＜y1，求m-n的取值范圍．
y
1
=
-
x
2
+
（
m
+
2
）
x
-
2
m
+
1
【考點(diǎn)】二次函數(shù)與不等式（組）；待定系數(shù)法求二次函數(shù)解析式．
【答案】（1）n=-3；
（2）點(diǎn)P是在拋物線(xiàn)y=x2-4x+5上運(yùn)動(dòng)；
（3）m-n≤1．
（2）點(diǎn)P是在拋物線(xiàn)y=x2-4x+5上運(yùn)動(dòng)；
（3）m-n≤1．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：516引用：1難度：0.6
相似題
-
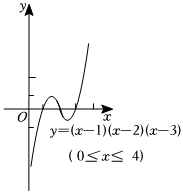1．如圖，是函數(shù)y=（x-1）（x-2）（x-3）（0≤x≤4）的圖象，通過(guò)觀(guān)察圖象得出了如下結(jié)論：
①當(dāng)x＞3時(shí)，y隨x的增大而增大；
②該函數(shù)圖象與坐標(biāo)軸有三個(gè)交點(diǎn)；
③該函數(shù)的最大值是6，最小值是-6；
④當(dāng)0≤x≤4時(shí)，不等式（x-1）（x-2）（x-3）＞0的解為1＜x＜2．
以上結(jié)論中正確的有（ ）發(fā)布：2025/5/22 7:0:2組卷：188引用：1難度：0.4 -
2．請(qǐng)閱讀下列解題過(guò)程；解一元二次不等式；x2-2x-3＜0．
解；設(shè)x2-2x-3=0，解得；x1=-1，x2=3．
則拋物線(xiàn)y=x2-2x-3與x軸的交點(diǎn)坐標(biāo)為（-1，0）和（3，0）．
畫(huà)出二次函數(shù)y=x2-2x-3的大致圖象（如圖1所示）．
由圖象可知；當(dāng)-1＜x＜3時(shí)函數(shù)圖象位于x軸下方，
此時(shí)y＜0，即x2-2x-3＜0．
所以一元二次不等式x2-2x-3＜0的解集為：-1＜x＜3．
通過(guò)對(duì)上述解題過(guò)程的學(xué)習(xí)，按其解題的思路和方法解答下列問(wèn)題：
（1）用類(lèi)似的方法解一元二次不等式；-x2+4x-3＞0．
（2）某“數(shù)學(xué)興趣小組”根據(jù)以上的經(jīng)驗(yàn)，對(duì)函數(shù)y=-（x-1）（|x|-3）的圖象和性質(zhì)進(jìn)行了探究，探究過(guò)程如下；
①列表；x與y的幾組對(duì)應(yīng)值如表，其中m=．
②如圖2，在直角坐標(biāo)系中畫(huà)出了函數(shù)y=-（x-1）（|x|-3）的部分圖象，用描點(diǎn)法將這個(gè)圖象補(bǔ)畫(huà)完整．x … -4 -3 -2 -1 0 1 2 3 4 … y … 5 0 -3 m -3 0 1 0 -3 …
③結(jié)合函數(shù)圖象，解決下列問(wèn)題；不等式-4≤-（x-1）（|x|-3）≤0的解集為：．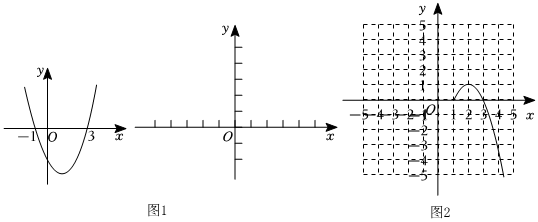
發(fā)布：2025/5/22 9:0:1組卷：980引用：3難度：0.3 -
3．已知二次函數(shù)y1=-x2+bx+c（b,c是常數(shù)）與一次函數(shù)y2=kx+c（k是常數(shù)，k≠0）．
（1）若y1的圖象與x軸只有一個(gè)交點(diǎn)（2，0），求b,c的值；
（2）若y1的圖象可由拋物線(xiàn)y=ax2+2c（a是常數(shù)，a≠0）向左平移2個(gè)單位，向上平移1個(gè)單位得到，求出y1的函數(shù)關(guān)系式；
（3）若k+b=3，當(dāng)x≥2時(shí)，y1＜y2恒成立，求k的取值范圍．發(fā)布：2025/5/21 22:30:1組卷：259引用：1難度：0.5
相關(guān)試卷