通過對如圖數學模型的研究學習，解決下列問題：
（1）如圖1，∠BAD=90°，AB=AD，過點B作BC⊥AC于點C，過點D作DE⊥AC于點E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D．又∠ACB=∠AED=90°，可以推理得到△ABC≌△DAE．進而得到AC=DEDE，BC=AE．我們把這個數學模型稱為“K字”模型或“一線三等角”模型；
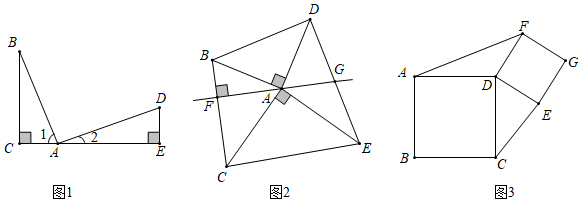
（2）如圖2，∠BAD=∠CAE=90°，AB=AD，AC=AE，連接BC，DE，且BC⊥AF于點F，DE與直線AF交于點G．求證：點G是DE的中點；
（深入探究）
（3）如圖，已知四邊形ABCD和DEGF為正方形，△AFD的面積為S1，△DCE的面積為S2，S1+S2=10，直接寫出S1的值．
【考點】四邊形綜合題．
【答案】DE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：853引用：3難度：0.1
相似題
-
1．已知，在?ABCD中，E為AB上一點，且DE=2AD，作∠ADE的平分線交AB于點F．
（1）如圖1，當E與B重合時，連接FC交BD于點G，若FC⊥CD，AF=3，求線段CF的長．
（2）如圖2，當CE⊥AB時，過點F作FH⊥BC于點H，交EC于點M．若G為FD中點，CE=2AF，求證：CD-3AG=EM．
（3）如圖3，在（1）的條件下，M為線段FC上一點，且CM=，P為線段CD上的一個動點，將線段MP繞著點M逆時針旋轉30°得到線段MP′，連接FP′，直接寫出FP′的最小值．3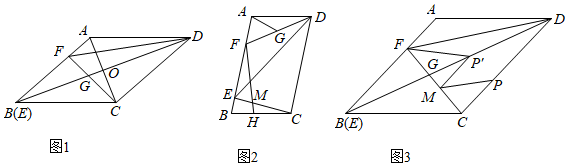
發布：2025/5/26 4:0:1組卷：481引用：2難度：0.1 -
2．如圖1，點O為矩形ABCD對角線AC的中點，AB=2，AD=2
．沿對角線AC將矩形剪開得到△ADC與△A′BC′，將△A′BC′繞點O逆時針旋轉α°（0＜α≤120），記BC′與OC的交點為P，如圖2．3
（1）①在圖2中，連接OB，OD，BD，則△OBD的形狀為 ；
②連接A′C，求證：A′C=BD；
（2）求OP長度的最小值；
（3）當△OPC′的內心在其一邊的垂直平分線上時，直接寫出α的值．
發布：2025/5/26 4:30:1組卷：83引用：2難度：0.3 -
3．問題情境：
在數學課上，老師給出了這樣一道題：如圖1，在△ABC中，AB=AC=6，∠BAC=30°，求BC的長．
探究發現：
（1）如圖2，勤奮小組經過思考后發現：把△ABC繞點A順時針旋轉90°得到△ADE，連接BD，BE，利用直角三角形的性質可求BC的長，其解法如下：
過點B作BH⊥DE交DE的延長線于點H，則BC=DE=DH-HE．
△ABC繞點A順時針旋轉90°得到△ADE，AB=AC=6，∠BAC=30°∴……
請你根據勤奮小組的思路，完成求解過程．
拓展延伸：
（2）如圖3，縝密小組的同學在勤奮小組的啟發下，把△ABC繞點A順時針旋轉120°后得到△ADE，連接BD，CE交于點F，交AB于點G，請你判斷四邊形ADFC的形狀并證明；
（3）奇異小組的同學把圖3中的△BGF繞點B順時針旋轉，在旋轉過程中，連接AF，發現AF的長度不斷變化，直接寫出AF的最大值和最小值．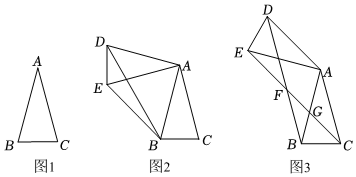
發布：2025/5/26 3:0:2組卷：83引用：1難度：0.3