設二次函數y=ax2+4ax+4a+1（a為常數，且a＜0）．
（1）寫出該函數的對稱軸和頂點坐標；
（2）若該函數圖象與直線y=1+9a有交點，求交點的橫坐標；
（3）若該函數圖象經過點P（x1，y1），Q（x2，y2），設n≤x1≤n+1，當x2≥1時均有y1≥y2，數n的取值范圍．
【答案】（1）對稱軸是直線x=-2，頂點為（-2，1）．
（2）-5或1．
（3）-5≤n≤0．
（2）-5或1．
（3）-5≤n≤0．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/29 8:0:10組卷：375引用：1難度：0.4
相似題
-
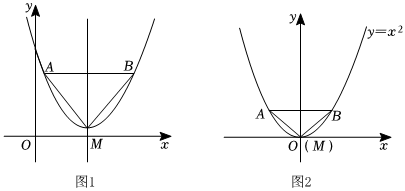
1．如圖1，拋物線的頂點為M，平行于x軸的直線與該拋物線交于點A，B（點A在點B左側），根據對稱性△AMB恒為等腰三角形，我們規定：當△AMB為直角三角形時，就稱△AMB為該拋物線的“完美三角形”．如圖2，則拋物線y=x2的“完美三角形”斜邊AB的長 ．
發布：2025/5/23 1:0:1組卷：618引用：10難度：0.5 -
2．已知點（-3，p），（1，q）都在二次函數y=ax2+bx+c（a＜0）的圖象上．設函數圖象的頂點橫坐標為m,當p=q時，m的值是 ；當p＜q＜c時，m的取值范圍是 ．
發布：2025/5/23 2:0:6組卷：566引用：3難度：0.6 -
3．已知二次函數y=-x2+6x-5．
（1）求二次函數圖象的頂點坐標；
（2）當1≤x≤4時，函數的最大值和最小值分別為多少？
（3）當t≤x≤t+3時，函數的最大值為m,最小值為n,若m-n=3，求t的值．發布：2025/5/22 23:30:1組卷：4850引用：12難度：0.6