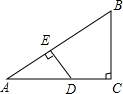
如圖，在△ABC中，∠C=90°，D是AC上一點(diǎn)，DE⊥AB于點(diǎn)E，若AC=8，BC=6，DE=3，則AD的長為（ ）
【考點(diǎn)】勾股定理；相似三角形的判定與性質(zhì)．
【答案】C
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/14 0:0:8組卷：576引用：38難度：0.9
相似題
-
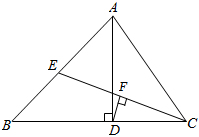1．如圖，在△ABC中，AD是BC邊上的高，CE是AB邊上的中線，DF⊥CE于F，CD=AE．
（1）求證：CF=EF；
（2）已知BC=13，CD=5，求△BEC的周長．發(fā)布：2025/5/26 9:0:1組卷：285引用：1難度：0.5 -
2．如圖，在Rt△ABC中，∠ACB=90°，AC=BC，過點(diǎn)C作CD⊥AB，垂足為D，點(diǎn)E為BC的中點(diǎn)，AE與CD交于點(diǎn)F，若DF的長為，則AE的長為（ ）√23發(fā)布：2025/5/26 7:30:2組卷：625引用：9難度：0.4 -
3．在△ABC中，∠C=90°，AC=8，
，點(diǎn)D為直線AB上一點(diǎn)，連接CD，若∠BCD=30°，則線段BD的長為 ．BC=4√3發(fā)布：2025/5/26 9:30:1組卷：195引用：2難度：0.5