在△ABC中，∠C=90°，AC=8，BC=43，點D為直線AB上一點，連接CD，若∠BCD=30°，則線段BD的長為 473或47473或47．
BC
=
4
3
4
7
3
7
4
7
3
7
【考點】勾股定理．
【答案】或4
4
7
3
7
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2025/5/26 9:30:1組卷：195引用：2難度：0.5
相似題
-
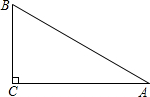1．Rt△ABC，∠C=90°，如圖，AC=8，AB=10，則邊BC=．發(fā)布：2025/5/28 1:0:2組卷：21引用：1難度：0.5 -
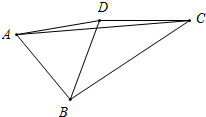2．如圖，四邊形ABCD中，∠BAD=60°，∠BCD=30°，AB=AD，BC=8cm,CD=5cm,則AC的長為cm.發(fā)布：2025/5/28 1:30:2組卷：147引用：2難度：0.5 -
3．清朝康熙皇帝是我國歷史上對數(shù)學很有興趣的帝王．近日，西安發(fā)現(xiàn)了他的數(shù)學專著，其中有一文《積求勾股法》，它對“三邊長為3、4、5的整數(shù)倍的直角三角形，已知面積求邊長”這一問題提出了解法：“若所設者為積數(shù)（面積），以積率六除之，平方開之得數(shù)，再以勾股弦各率乘之，即得勾股弦之數(shù)”．用現(xiàn)在的數(shù)學語言表述是：“若直角三角形的三邊長分別為3、4、5的整數(shù)倍，設其面積為S，則第一步：
=m；第二步：S6=k；第三步：分別用3、4、5乘k,得三邊長”．m
（1）當面積S等于150時，請用康熙的“積求勾股法”求出這個直角三角形的三邊長；
（2）你能證明“積求勾股法”的正確性嗎請寫出證明過程．發(fā)布：2025/5/28 1:0:2組卷：615引用：14難度：0.1