在△ABC中，∠ACB=90°，AC=BC=2，把△ABC繞點B順時針旋轉得到△DBE（點A與D對應）．
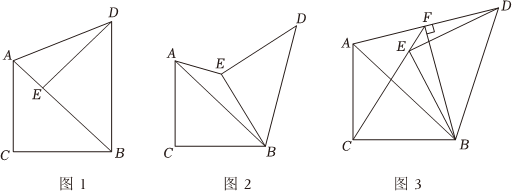
（1）如圖1，若點E落在邊AB上，連接AD，求AE的長；
（2）如圖2，若旋轉角度為60°，連接AE．求AE的長；
（3）如圖3，若旋轉角度為α（45°≤α≤90°），連接AD，BF⊥AD，垂足為F．求證：C，E，F三點在同一直線上．
【考點】幾何變換綜合題．
【答案】（1）；
（2）；
（3）證明見解析．
2
2
-
2
（2）
6
-
2
（3）證明見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/26 18:0:2組卷：52引用：2難度：0.5
相似題
-
1．如圖，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=2，在平面內將線段AC繞點A順時針旋轉至線段AD的位置，E是BD的中點．
（1）如圖1，若∠CAD=60°，求AE的長；
（2）如圖2，若∠CAD=120°，猜想AE與BC的數量關系，并證明你猜想的結論；
（3）如圖3，點B關于直線AC的對稱點為F，在線段AC的旋轉過程中，當EF的長取得最小值時，請直接寫出△BCD的面積．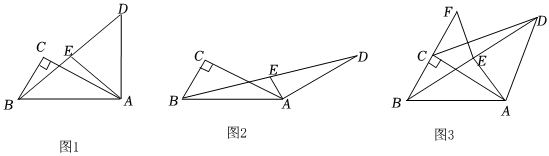
發布：2025/5/21 15:30:1組卷：356引用：1難度：0.3 -
2．如圖，甲、乙分別從A（-9，0），B（13，0）兩點同時出發，甲朝著正北方向，以每秒3個單位長度的速度運動；乙朝著正西方向，以每秒4個單位長度的速度運動，設運動時間為t秒．
規定：t秒時，甲到達的位置記為點At，乙到達的位置記為點Bt，例如，1秒時，甲到達的位置記為A1，乙到達的位置記為B1（如圖所示）；2.5秒時，甲到達的位置記為A2.5等等，容易知道，兩條平行且相等的線段，其中包含有相同的方位信息，所以，在研究有關運動問題時，為研究方便，我們可把點或線段進行合適的平移后，再去研究（物理上的相對運動觀，就是源于這種數學方法），現對t秒時，甲、乙到達的位置點At，Bt，按如下步驟操作：
第一步：連接AtBt；
第二步：把線段AtBt進行平移，使點Bt與點B重合，平移后，點At的對應點用點At′標記．
?
解答下列問題：
（1）[理解與初步應用]當t=1時，
①利用網格，在圖中畫出A1，B1經過上述第二步操作后的圖形；
②此時，甲在乙的什么方位？（請填空）
答：此時，甲在乙的北偏西θ°（其中tanθ°=），兩者相距 個單位長度．
（2）[實驗與數據整理]補全表格：
（3）[數據分析與結論運用]t的取值 1 2 3 t 點At′的坐標 （-5，3） （ ，） （ ，） （ ，）
①如果把點At′的橫、縱坐標分別用變量x,y表示，則y與x之間的函數關系式為 ；
②點A3.5′的坐標為 ．
（4）[拓展應用]我們知道，在運動過程中的任意時刻t,甲相對于乙的方位（即，點At相對于點Bt的方位）與At′相對于點B的方位相同，這為我們解決某些問題，提供了新思路．
請解答：運動過程中，甲、乙之間的最近距離為 個單位長度．發布：2025/5/21 12:30:1組卷：274引用：1難度：0.1 -
3．【問題探究】
（1）如圖1，△ABC和△DEC均為等腰直角三角形，∠ACB=∠DCE=90°，點B，D，E在同一直線上，連接AD，BD．
①請探究AD與BD之間的位置關系：；
②若AC=BC=，DC=CE=10，則線段AD的長為；2
【拓展延伸】
（2）如圖2，△ABC和△DEC均為直角三角形，∠ACB=∠DCE=90°，AC=，BC=21，CD=7，CE=1．將△DCE繞點C在平面內順時針旋轉，設旋轉角∠BCD為α（0°≤α＜360°），作直線BD，連接AD，當點B，D，E在同一直線上時，畫出圖形，并求線段AD的長．3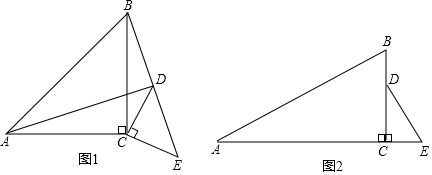
發布：2025/5/21 15:0:1組卷：4033引用：10難度：0.3