當前位置：
章節挑題
請展開查看知識點列表
>
更多>>
|
原創
更新中
|
知識圖解
新知探究
答疑解惑
針對訓練
瀏覽次數：6763
更新：2025年06月06日
|
|
原創
已完結
|
解題模型
因材施教
夯實基礎
穩步提升
瀏覽次數：13917
更新：2025年06月04日
|
2801．如圖①，△ABC中，BD平分∠ABC，且與△ABC的外角∠ACE的角平分線交于點D．
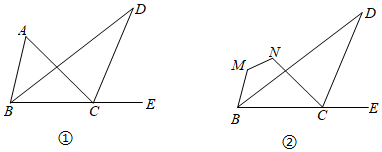
（1）若∠ABC=70°，∠ACB=40°，求∠D的度數；
（2）若把∠A截去，得到四邊形MNCB，如圖②，猜想∠D、∠M、∠N的關系，并說明理由．發布：2024/6/27 10:35:59組卷：932引用：3難度：0.52802．觀察以下等式：
（x+1）（x2-x+1）=x3+1
（x+3）（x2-3x+9）=x3+27
（x+6）（x2-6x+36）=x3+216
…
（1）按以上等式的規律，填空：（a+b）（ ）=a3+b3；
（2）利用多項式的乘法法則，說明（1）中的等式成立；
（3）利用（1）中的公式化簡：（x+y）（x2-xy+y2）-（x+2y）（x2-2xy+4y2）．發布：2024/6/27 10:35:59組卷：5975引用：17難度：0.3
2803．如圖，∠BAC=90°，AD是∠BAC內部一條射線，若AB=AC，BE⊥AD于點E，CF⊥AD于點F．求證：AF=BE．發布：2024/6/27 10:35:59組卷：1349引用：14難度：0.72804．如圖1所示，從邊長為a的正方形紙片中剪去一個邊長為b的小正方形，再沿著線段AB剪開，把剪成的兩張紙拼成如圖2的等腰梯形（其面積=
（上底+下底）×高）．12
（1）設圖1中陰影部分面積為S1，圖2中陰影部分面積為S2，請直接用含a、b的式子表示S1和S2；
（2）請寫出上述過程所揭示的乘法公式．發布：2024/6/27 10:35:59組卷：2803引用：61難度：0.5
2805．如圖1是一個長為4a、寬為b的長方形，沿圖中虛線用剪刀平均分成四塊小長方形，然后用四塊小長方形拼成一個“回形”正方形（如圖2）
（1）觀察圖2請你寫出（a+b）2、（a-b）2、ab之間的等量關系是；
（2）根據（1）中的結論，若x+y=5，x?y=，則x-y=；94
（3）拓展應用：若（2019-m）2+（m-2020）2=7，求（2019-m）（m-2020）的值．發布：2024/6/27 10:35:59組卷：2257引用：12難度：0.72806．在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E．
（1）當直線MN繞點C旋轉到圖1的位置時，求證：
①△ADC≌△CEB；
②DE=AD+BE；
（2）當直線MN繞點C旋轉到圖2的位置時，求證：DE=AD-BE；
（3）當直線MN繞點C旋轉到圖3的位置時，試問DE、AD、BE具有怎樣的等量關系？請寫出這個等量關系，并加以證明．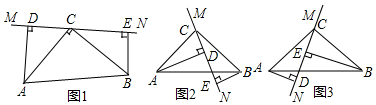
發布：2024/6/27 10:35:59組卷：6101引用：53難度：0.5
2807．如圖，已知△ACF≌△DBE，且點A，B，C，D在同一條直線上，∠A=50°，∠F=40°．
（1）求△DBE各內角的度數；
（2）若AD=16，BC=10，求AB的長．發布：2024/6/27 10:35:59組卷：3054引用：10難度：0.3
2808．如圖，△ACB中，∠ACB=90°，∠1=∠B．
（1）試說明CD是△ABC的高；
（2）如果AC=8，BC=6，AB=10，求CD的長．發布：2024/6/27 10:35:59組卷：4441引用：27難度：0.5
2809．如圖，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CF，垂足為F．
（1）求證：△ABC≌△ADE；
（2）若AC=10，求四邊形ABCD的面積；
（3）求∠FAE的度數．發布：2024/6/27 10:35:59組卷：2054引用：14難度：0.62810．隨著“和諧號”列車緩緩停靠在梅州西站，我市正式進入了高鐵時代．與普通列車相比，“和諧號”列車時速更快，安全性更好．已知“梅州西-廣州南”全程大約480千米，“和諧號”D7315次列車平均每小時比普通列車多行駛40千米，其行駛時間是普通列車行駛時間的
（兩列車中途停留時間均除外）．34
（1）經查詢，“和諧號”D7315次列車從梅州西到廣州南，中途合計停站時間為20分鐘，求乘坐“和諧號”D7315次列車從梅州西到廣州南需要多長時間；
（2）據了解，梅州西站后期還會引進更快的“復興號”高鐵，屆時跑完480千米的路程最多只需要2.5小時，請問“復興號”高鐵的速度每小時至少比“和諧號”列車快了多少千米？發布：2024/6/27 10:35:59組卷：311引用：3難度：0.7
