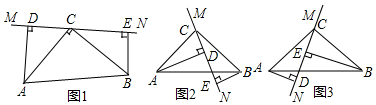
在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E．
（1）當直線MN繞點C旋轉到圖1的位置時，求證：
①△ADC≌△CEB；
②DE=AD+BE；
（2）當直線MN繞點C旋轉到圖2的位置時，求證：DE=AD-BE；
（3）當直線MN繞點C旋轉到圖3的位置時，試問DE、AD、BE具有怎樣的等量關系？請寫出這個等量關系，并加以證明．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：6089引用：53難度：0.5

相似題

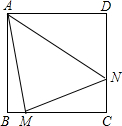1．如圖，在正方形ABCD中，M、N各在BC和CD上，滿足∠MAN=45°
求證：S_△AMN=S_△ABM+S_△ADN．
發布：2025/5/28 9:30:2組卷：322引用：1難度：0.5
解析
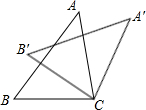2．如圖，把△ABC繞點C順時針旋轉得到△A′B′C，此時A′B′⊥AC于D，已知∠B′CB=28°，則∠A的度數是（　　）
A．34° B．56° C．62° D．78°
發布：2025/5/28 8:0:1組卷：116引用：2難度：0.9
解析
3．如圖，在正方形ABCD中，E是CD邊的中點，點F在BC上，∠EAF=∠DAE，則下列結論中正確的是（　　）
A．∠EAF=∠FAB B．BC=3FC C．AF=AE+FC D．AF=BC+FC
發布：2025/5/28 10:0:1組卷：745引用：8難度：0.9
解析

相關試卷

1．如圖，在正方形ABCD中，M、N各在BC和CD上，滿足∠MAN=45°求證：S△AMN=S△ABM+S△ADN．