小輝同學觀看2022卡塔爾世界杯時發現，優秀的球員通常都能選擇最優的點射門（僅從射門角度大小考慮）．這引起了小輝同學的興趣，于是他展開了一次有趣的數學探究．
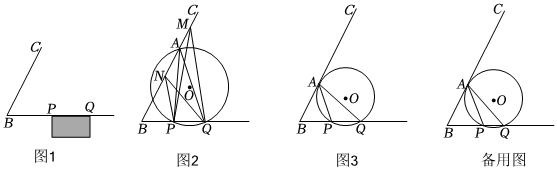
【提出問題】如圖1所示．球員帶球沿直線BC奔向球門PQ，
探究：是否存在一個位置，使得射門角度最大．
【分析問題】因為線段PQ長度不變，我們聯想到圓中的弦和圓周角．
如圖2，射線BC與⊙O相交，點M，點A，點N分別在圓外、圓上、圓內，連接NP，NQ，AP，AQ，MP，MQ．
【解決問題】
（1）如圖2，比較∠PMQ、∠PAQ、∠PNQ的大小：∠PMQ＜∠PAQ＜∠PNQ∠PMQ＜∠PAQ＜∠PNQ（用“＜”連接起來）．
（2）如圖3，點A是射線BC上一動點（點A不與點B重合）．證明：當△APQ的外接圓⊙O與射線BC相切時，∠PAQ最大．
（3）【延伸拓展】在（2）的條件下，如果PQ=4，PB=5，tanB=2．當∠PAQ最大時．證明：∠PAQ=90°-∠B．
【考點】圓的綜合題．
【答案】∠PMQ＜∠PAQ＜∠PNQ
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：164引用：2難度：0.1
相似題
-
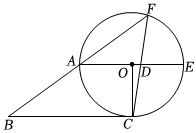1．如圖，四邊形OABC中，AO∥BC，∠AOC=90°，AO=3，AB=5．以O為圓心，OA為半徑作圓，⊙O經過點C，且與BA的延長線交于F．延長AO交圓于E，連接FC交AE于點D．
（1）求證：BC是⊙O的切線；
（2）求cos∠FAE的值；
（3）求線段OD的長．發布：2025/6/7 5:0:1組卷：79引用：1難度：0.3 -
2．等腰三角形AFG中AF=AG，且內接于圓O，D、E為邊FG上兩點（D在F、E之間），分別延長AD、AE交圓O于B、C兩點（如圖1），記∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）連接CF，交AB于H（如圖2）．若β=45°，且BC×EF=AE×CF．求證：∠AHC=2∠BAC；
（3）在（2）的條件下，取CH中點M，連接OM、GM（如圖3），若∠OGM=2α-45°，
①求證：GM∥BC，GM=BC；12
②請直接寫出的值．OMMC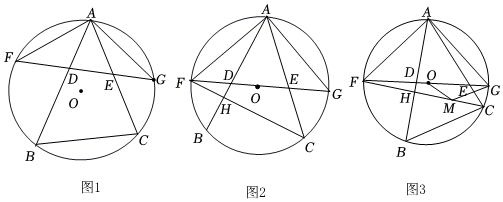
發布：2025/6/7 16:0:2組卷：1490引用：8難度：0.1 -
3．已知，線段AB是⊙O的直徑，弦CD⊥AB于點H，點M是優弧CBD上的任意一點，AH=2，CH=4．
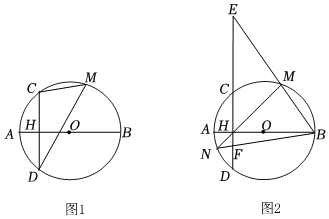
（1）如圖1，
①求⊙O的半徑；
②求sin∠CMD的值．
（2）如圖2，直線BM交直線CD于點E，直線MH交⊙O于點N，連結BN交CD于點F，求HE?FH的值．發布：2025/6/7 7:0:1組卷：476引用：2難度：0.3