2023年廣東省珠海市香洲區中考數學二模試卷
發布：2024/4/23 12:26:7
一、選擇題（本大題10小題，每小題3分，共30分）每小題給出四個選項中只有一個是正確的，請把答題卡上對應題目所選的選項涂黑．
-
1．2023的相反數是（ ）
組卷：5365引用：291難度：0.8 -
2．將y=x2向上平移2個單位后所得的拋物線的解析式為（ ）
組卷：926引用：15難度：0.9 -
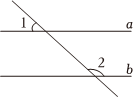3．如圖，直線a∥b,∠1=40°，則∠2=（ ）組卷：116引用：3難度：0.9 -
4．圓錐的底面半徑為3，母線長為5．則這個圓錐的側面積為（ ）
組卷：566引用：7難度：0.8 -
5．下列計算正確的是（ ）
組卷：295引用：4難度：0.8 -
6．若一元二次方程x2-2x+a=0有一根為-1，則另一根為（ ）
組卷：206引用：5難度：0.7 -
7．如圖，電線桿AB的中點C處有一標志物，在地面D點處測得標志物的仰角為35°，若拉線CD的長度是a米，則電線桿AB的長可表示為（ ）組卷：280引用：4難度：0.5
五、解答題（三）（本大題2小題，每小題12分，共24分）
-
22．在平面直角坐標系xOy中，已知拋物線L：y=x2-2x+2-m和線段AB，其中點A（0，1），點B（5，6），點C是拋物線L與y軸的交點，點D是拋物線L的頂點．
（1）求直線AB的解析式；
（2）點Q在拋物線L上，且與點C關于對稱軸對稱，連接CD，DQ，CQ，求證：△CDQ為等腰直角三角形；
（3）在（2）的條件下，射線DQ交x軸于點F，連接DA，BF，四邊形ABFD是否能構成平行四邊形？如果能，請求m的值；如果不能，說明理由；
（4）若拋物線L與線段AB只有一個交點．請結合函數圖象，直接寫出m的取值范圍 ．組卷：184引用：3難度：0.1 -
23．小輝同學觀看2022卡塔爾世界杯時發現，優秀的球員通常都能選擇最優的點射門（僅從射門角度大小考慮）．這引起了小輝同學的興趣，于是他展開了一次有趣的數學探究．
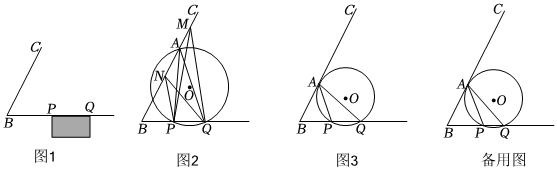
【提出問題】如圖1所示．球員帶球沿直線BC奔向球門PQ，
探究：是否存在一個位置，使得射門角度最大．
【分析問題】因為線段PQ長度不變，我們聯想到圓中的弦和圓周角．
如圖2，射線BC與⊙O相交，點M，點A，點N分別在圓外、圓上、圓內，連接NP，NQ，AP，AQ，MP，MQ．
【解決問題】
（1）如圖2，比較∠PMQ、∠PAQ、∠PNQ的大小：（用“＜”連接起來）．
（2）如圖3，點A是射線BC上一動點（點A不與點B重合）．證明：當△APQ的外接圓⊙O與射線BC相切時，∠PAQ最大．
（3）【延伸拓展】在（2）的條件下，如果PQ=4，PB=5，tanB=2．當∠PAQ最大時．證明：∠PAQ=90°-∠B．組卷：164引用：2難度：0.1