已知拋物線y=ax2+4ax-12a（a為常數，a＜0）與x軸相交于點A，點B（點A在點B的左側），與y軸相交于點C，點D是該拋物線的頂點．
（Ⅰ）當a=-1時，求點C，D的坐標；
（Ⅱ）直線x=m（m是常數）與拋物線相交于第二象限的點P，與AC相交于點Q，當PQ的最大值為92時，求拋物線的解析式；
（Ⅲ）將線段AC沿x軸方向平移至A'C'，A′為點A的對應點，C′為點C的對應點，連接DA′，OC'，當a為何值時，DA'+OC'的最小值為5，并求此時點C的坐標．
9
2
【考點】二次函數綜合題．
【答案】（Ⅰ）C（0，12），D（-2，16）；
（Ⅱ）拋物線的解析式為；
（Ⅲ）當時，DA'+OC'的最小值為5，此時，C．
（Ⅱ）拋物線的解析式為
y
=
-
1
2
x
2
-
2
x
+
6
（Ⅲ）當
a
2
=
-
3
28
（
0
，
9
7
）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/23 12:26:7組卷：729引用：1難度：0.4
相似題
-
1．如圖，在平面直角坐標系中，拋物線y=-x2-2x+c（c為常數）與一次函數y=-x+b（b為常數）交于A、B兩點，其中A點坐標為（-3，0）．
（1）求B點坐標；
（2）點P為直線AB上方拋物線上一點，連接PA，PB，當S△PAB=時，求點P的坐標；1258
（3）將拋物線y=-x2-2x+c（c為常數）沿射線AB平移5個單位，平移后的拋物線y1與原拋物線y=-x2-2x+c相交于點E，點F為拋物線y1的頂點，點M為y軸上一點，在平面直角坐標系中是否存在點N，使得以點E，F，M，N為頂點的四邊形是菱形，若存在，請直接寫出點N的坐標；若不存在，請說明理由．2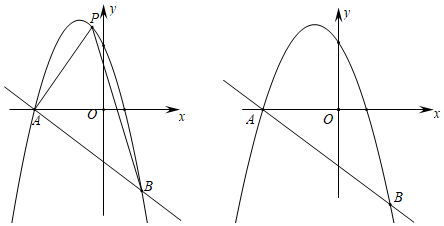
發布：2025/6/9 22:30:2組卷：485引用：5難度：0.1 -
2．在平面直角坐標系xOy中，拋物線y=x2+bx+c（b、c為常數）經過點A（0，-3）和點B（3，0），點M在此拋物線，點M的橫坐標為m,點M不與A、B重合．
（1）求此拋物線所對應的函數表達式．
（2）當S△OAM=2S△AOB，求點M的坐標．
（3）作點A關于拋物線對稱軸的對稱點為點C，當點M到直線AC的距離是點M到x軸距離2倍時，求m的值．
（4）設點E的坐標為（-m-2，m），點F的坐標為（2m-2，m），連接EF．當拋物線在B、M兩點之間的部分（包含B、M兩點）與線段EF有1個公共點時，直接寫出m的取值范圍．發布：2025/6/9 23:30:1組卷：125引用：3難度：0.2 -
3．【生活情境】
為美化校園環境，某學校根據地形情況，要對景觀帶中一個長AD=4m,寬AB=1m的長方形水池ABCD進行加長改造（如圖①，改造后的水池ABNM仍為長方形，以下簡稱水池1）．同時，再建造一個周長為12m的矩形水池EFGH（如圖②，以下簡稱水池2）．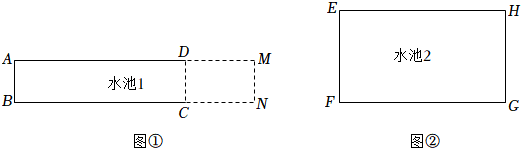
【建立模型】
如果設水池ABCD的邊AD加長長度DM為x（m）（x＞0），加長后水池1的總面積為y1（m2），則y1關于x的函數解析式為：y1=x+4（x＞0）；設水池2的邊EF的長為x（m）（0＜x＜6），面積為y2（m2），則y2關于x的函數解析式為：y2=-x2+6x（0＜x＜6），上述兩個函數在同一平面直角坐標系中的圖象如圖③．
【問題解決】
（1）若水池2的面積隨EF長度的增加而減小，則EF長度的取值范圍是 （可省略單位），水池2面積的最大值是 m2；
（2）在圖③字母標注的點中，表示兩個水池面積相等的點是 ，此時的x（m）值是 ；
（3）當水池1的面積大于水池2的面積時，x（m）的取值范圍是 ；
（4）在1＜x＜4范圍內，求兩個水池面積差的最大值和此時x的值；
（5）假設水池ABCD的邊AD的長度為b（m），其他條件不變（這個加長改造后的新水池簡稱水池3），則水池3的總面積y3（m2）關于x（m）（x＞0）的函數解析式為：y3=x+b（x＞0）．若水池3與水池2的面積相等時，x（m）有唯一值，求b的值．發布：2025/6/10 0:0:1組卷：1987引用：6難度：0.3
相關試卷