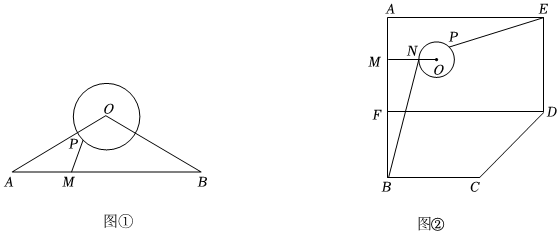
（1）如圖①，在△OAB中，OA=OB，∠AOB=120°，AB=24．若⊙O的半徑為4，點P在⊙O上，點M在AB上，連接PM，求線段PM的最小值；
（2）如圖②所示，五邊形ABCDE是某市工業新區的外環路，新區管委會在點B處，點E處是該市的一個交通樞紐．已知：∠A=∠ABC=∠AED=90°，AB=AE=10000m,BC=DE=6000m.根據新區的自然環境及實際需求，現要在矩形AFDE區域內（含邊界）修一個半徑為30m的圓型環道⊙O；過圓心O，作OM⊥AB，垂足為M，與⊙O交于點N．連接BN，點P在⊙O上，連接EP．其中，線段BN、EP及MN是要修的三條道路，要在所修道路BN、EP之和最短的情況下，使所修道路MN最短，試求此時環道⊙O的圓心O到AB的距離OM的長．
【考點】圓的綜合題．
【答案】（1）4-4；
（2）4047.91m．
3
（2）4047.91m．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/15 8:0:8組卷：1733引用：1難度：0.5
相似題
-
1．如圖1，以點O為圓心，半徑為4的圓交x軸于A，B兩點，交y軸于C，D兩點，點P為劣弧AC上的一動點，延長CP交x軸于點E；連接PB，交OC于點F．
（1）若點F為OC的中點，求PB的長；
（2）求CP?CE的值；
（3）如圖2，過點O作OH∥AP交PD于點H，當點P在弧AC上運動時，連接AC，PC．試問△APC與△OHD相似嗎？說明理由；的值是否保持不變？若不變，試證明，求出它的值；若發生變化，請說明理由．APDH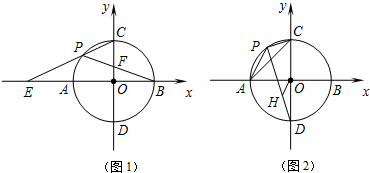
發布：2025/6/24 18:30:1組卷：272引用：1難度：0.5 -
2．如圖，已知⊙O′與x軸交于A、B兩點，與y軸交于C、D兩點，圓心O′的坐標是（1，-1），半徑為．5
（1）比較線段AB與CD的大小；
（2）求A、B、C、D四點的坐標；
（3）過點D作⊙O′的切線，試求這條切線的解析式．發布：2025/6/24 20:0:2組卷：43引用：1難度：0.5 -
3．下面是“用三角板畫圓的切線”的畫圖過程．
如圖1，已知圓上一點A，畫過A點的圓的切線．畫法：
（1）如圖2，將三角板的直角頂點放在圓上任一點C（與點A不重合）處，使其一直角邊經過點A，另一條直角邊與圓交于B點，連接AB；
（2）如圖3，將三角板的直角頂點與點A重合，使一條直角邊經過點B，畫出另一條直角邊所在的直線AD．則直線AD就是過點A的圓的切線．
請回答：①這種畫法是否正確 （是或否）；
②你判斷的依據是：．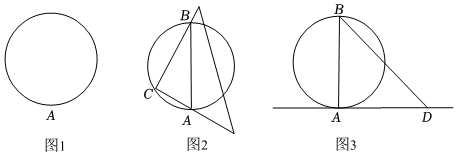
發布：2025/6/25 8:0:1組卷：19引用：1難度：0.4
相關試卷