小華是一個善于思考的同學．學習直線和圓的位置關系時，她知道了如何過圓上一點作圓的切線，課后通過動手操作，她發現過圓內一點作不出圓的切線，過圓外一點可以作出圓的兩條切線．下面是她過圓外一點作圓的兩條切線的方法：
已知：⊙O和⊙O外一點P；
求作：過點P作⊙O的切線．
作法：①連接OP；
②作線段OP的垂直平分線MN，垂足為C；
③以點C為圓心，CO為半徑畫圓，交⊙O于點A，B；
④作直線PA，PB，則直線PA，PB即為所求．
（1）根據小華的作法，完善上面作圖（保留作圖痕跡）；
（2）為了說明這一方法的正確性，需要對其進行證明，請給出證明過程．
【答案】（1）見解答；
（2）見解答．
（2）見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 1:0:1組卷：49引用：1難度：0.5
相似題
-
1．已知：四邊形ABCD．
求作：直線CE，使得CE∥AB，交AD于點E．發布：2025/6/4 19:30:1組卷：251引用：4難度：0.6 -
2．已知∠α、∠β，求作∠AOB，使∠AOB=∠α-∠β．發布：2025/6/4 20:0:1組卷：248引用：8難度：0.3 -
3．數學課上，老師要求同學們利用三角板畫出兩條平行線，老師展示了甲、乙兩位同學的畫法如下：
甲的畫法：
乙的畫法：①將含30°角的三角尺的最長邊與直線a重合，另一塊三角尺最長邊與含30°角的三角尺的最短邊緊貼；
②將含30°角的三角尺沿貼合邊平移一段距離，畫出最長邊所在直線b,則b∥a.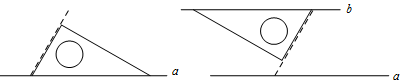
請你判斷兩人的作圖的正確性（ ）①將含30°角三角尺的最長邊與直線a重合，用虛線作出一條最短邊所在直線；
②再次將含30°角三角尺最短邊與虛線重合，畫出最長邊所在直線b,則b∥a.發布：2025/6/4 20:30:1組卷：144引用：4難度：0.7