如圖所示，I為△ABC的內(nèi)心，求證：△BIC的外心O與A、B、C四點(diǎn)共圓．
【考點(diǎn)】四點(diǎn)共圓；三角形的五心．
【答案】見試題解答內(nèi)容
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/27 14:0:0組卷：319引用：1難度：0.9
相似題
-
1．綜合與實(shí)踐：
“善思”小組開展“探究四點(diǎn)共圓的條件”活動(dòng)，得出結(jié)論：對(duì)角互補(bǔ)的四邊形四個(gè)頂點(diǎn)共圓．該小組繼續(xù)利用上述結(jié)論進(jìn)行探究．
提出問(wèn)題：
如圖1所示，在線段AC同側(cè)有兩點(diǎn)B，D，連接AD，AB，BC，CD，如果∠B=∠D，那么A，B，C，D四點(diǎn)在同一個(gè)圓上．
探究展示：
如圖2所示，作經(jīng)過(guò)點(diǎn)A，C，D的⊙O，在劣弧AC上取一點(diǎn)E（不與A，C重合），連接AE，CE，則∠AEC+∠D=180°，（依據(jù)1）
∵∠B=∠D，
∴∠AEC+∠B=180°，
∴點(diǎn)A，B，C，E四點(diǎn)在同一個(gè)圓上，（對(duì)角互補(bǔ)的四邊形四個(gè)頂點(diǎn)共圓）
∴點(diǎn)B，D在點(diǎn)A，C，E所確定的⊙O上，（依據(jù)2）
∴點(diǎn)A，B，C，D四點(diǎn)在同一個(gè)圓上；
反思?xì)w納：
?（1）上述探究過(guò)程中的“依據(jù)1”、“依據(jù)2”分別是指什么？①圓內(nèi)接四邊形對(duì)角互補(bǔ)；
②對(duì)角互補(bǔ)的四邊形四個(gè)頂點(diǎn)共圓；
③過(guò)不在同一直線上的三個(gè)點(diǎn)有且只有一個(gè)圓；
④經(jīng)過(guò)兩點(diǎn)的圓的圓心在這兩點(diǎn)所連線段的垂直平分線上；
依據(jù)1：；（從框內(nèi)選一個(gè)選項(xiàng)，直接填序號(hào)）
依據(jù)2：．（從框內(nèi)選一個(gè)選項(xiàng)，直接填序號(hào)）
（2）如圖3所示，在四邊形ABCD中，∠1=∠2=80°，∠3=42°，則∠4的度數(shù)為 ．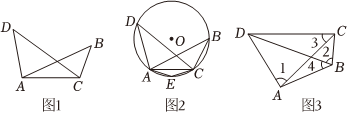
?發(fā)布：2024/9/21 14:0:9組卷：278引用：1難度：0.4 -
2．請(qǐng)仔細(xì)閱讀以下材料：
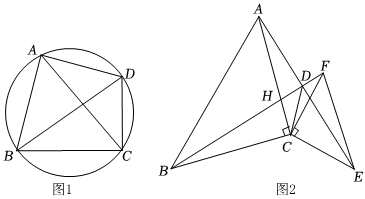
定理一：一般地，如圖1，四邊形ABCD中，如果連接兩條對(duì)角線后形成的∠BAC=∠BDC，則A，B，C，D四點(diǎn)共圓．我們由定理可以進(jìn)一步得出結(jié)論：∠BDA=∠BCA，∠DBC=∠DAC，∠ACD=∠ABD．
定理二：直角三角形斜邊上的中線等于斜邊的一半．
溫馨提示：下面問(wèn)題的關(guān)鍵地方或許能夠用到上述定理，如果用到，請(qǐng)直接運(yùn)用相關(guān)結(jié)論；如果你有自己更好的做法，那就以自己的做法為主，只要正確，一樣得分．
探究問(wèn)題：如圖2，在△ABC和△EFC中，AC=BC，EC=FC，∠ACB=∠ECF=90°，連接BF，AE交于點(diǎn)D，BF交AC于點(diǎn)H，連接CD．
（1）求證BF=AE；
（2）請(qǐng)直接寫出∠ADB=度，∠BDC=度；
（3）若∠DBC=15°，求證AH=2CD．發(fā)布：2024/8/6 8:0:9組卷：422引用：3難度：0.1 -
3．請(qǐng)閱讀以下材料，完成相應(yīng)任務(wù)．
我們知道，過(guò)任意一個(gè)三角形的三個(gè)頂點(diǎn)能作一個(gè)圓，那么過(guò)任意一個(gè)四邊形的四個(gè)頂點(diǎn)能作一個(gè)圓嗎？李雷經(jīng)過(guò)實(shí)踐探究發(fā)現(xiàn)了如下結(jié)論：
如果線段同側(cè)兩點(diǎn)（與線段在同一平面內(nèi)）分別與線段兩端點(diǎn)的連線所組成的夾角相等，那么這兩點(diǎn)和線段兩端點(diǎn)四點(diǎn)共圓．下面是李雷證明上述命題的過(guò)程（不完整）．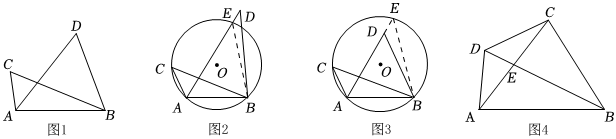
已知：如圖1，點(diǎn)C，D是線段AB同側(cè)兩點(diǎn)，且∠ACB=∠ADB．
求證：點(diǎn)A，B，C，D四點(diǎn)共圓．
證明：作△ABC的外接圓⊙O，假設(shè)點(diǎn)D在⊙O外或在⊙O內(nèi)．
如圖2，若點(diǎn)D在⊙O外．設(shè)AD與⊙O交于點(diǎn)E，連接BE，
則∠ACB=∠AEB（依據(jù)一），
又∵∠AEB=∠ADB+∠DBE（依據(jù)二），
∴∠ACB=∠ADB+∠DBE．
∴∠ACB＞∠ADB．這與已知條件“∠ACB=∠ADB”矛盾，故點(diǎn)D在⊙O外不成立；
如圖3，若點(diǎn)D在⊙O內(nèi)，……
（請(qǐng)同學(xué)們補(bǔ)充完整省略的部分證明過(guò)程）
綜上所述，作△ABC的外接圓⊙O，點(diǎn)D在⊙O上，即點(diǎn)A，B，C，D四點(diǎn)共圓．
（1）填空：將材料中依據(jù)一、依據(jù)二補(bǔ)充完整；
依據(jù)一：；
依據(jù)二：．
（2）請(qǐng)按照上面的證明思路，寫出該證明的剩余部分；
（3）填空：如圖4，在四邊形ABCD中，∠ABD=∠ACD，對(duì)角線AC，BD交于點(diǎn)E，E為AC中點(diǎn)，若BD=6，BE=4，則AC=．發(fā)布：2025/5/24 6:0:2組卷：698引用：1難度：0.3
相關(guān)試卷