【活動回顧】：八年級下冊教材中，我們曾探究過“函數y=2x-5的圖象上點的坐標的特征”，了解了一元一次不等式的解集與相應的一次函數圖象上點的坐標的關系．
發現：一元一次不等式2x-5＞0的解集是函數y=2x-5圖象在x軸上方的點的橫坐標的集合．
結論：一元一次不等式：kx+b＞0（或kx+b＜0）的解集，是函數y=kx+b圖象在x軸上方（或x軸下方）部分的點的橫坐標的集合．
【解決問題】：
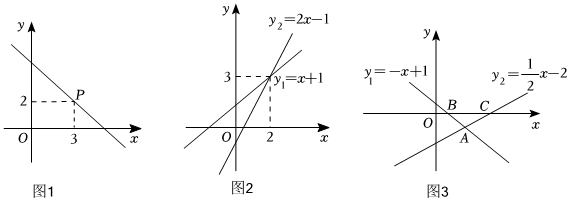
（1）如圖1，一次函數y=kx+b（k＜0）的圖象經過點P（3，2），則不等式kx+b＜2的解集是 x＞3x＞3．
（2）如圖2，兩條直線的交點坐標為 （2，3）（2，3），方程2x-1=x+1的解是 x=2x=2；不等式2x-1＞x+1的解是 x＞2x＞2．
【拓展延伸】
（3）如圖3，一次函數y1=-x+1和y2=12x-2的圖象相交于點A，分別與x軸相交于點B和點C．
①求點A，C的坐標；
②結合圖象，直接寫出關于x的不等式組12x-2＞-x+1 12x-2＞0
的解集是 x＞4x＞4．
y
2
=
1
2
x
-
2
1 2 x - 2 ＞ - x + 1 |
1 2 x - 2 ＞ 0 |
【答案】x＞3；（2，3）；x=2；x＞2；x＞4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/30 8:0:9組卷：471引用：4難度：0.5
相似題
-
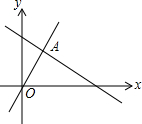1．如圖，函數y=2x和y=ax+4的圖象相交于點A（m,3），則不等式2x＜ax+4的解集為（ ）發布：2025/6/24 13:0:11組卷：925引用：13難度：0.7 -
2．畫出函數y1=2x-4與y2=-2x+8的圖象，觀察圖象并回答問題：
（1）x取何值時，2x-4＞0？
（2）x取何值時，-2x+8＞0？
（3）x取何值時，2x-4＞0與-2x+8＞0同時成立？
（4）你能求出函數y1=2x-4與y2=-2x+8的圖象與x軸所圍成的三角形的面積嗎？發布：2025/6/24 15:0:1組卷：1039引用：5難度：0.7 -
3．如圖，直線y=-x+m與y=nx+4n（n≠0）的交點的橫坐標為-2，則關于x的不等式-x+m＞nx+4n＞0的整數解為（ ）發布：2025/6/24 11:0:1組卷：8440引用：73難度：0.7