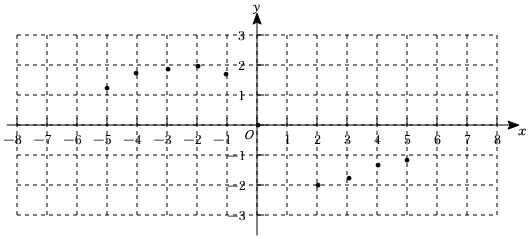
函數圖象是研究函數的重要工具，探究函數性質時，我們經歷了列表、描點、連線畫出函數圖象，然后觀察分析圖象特征，概括函數性質的過程．請結合已有的學習經驗，畫出函數y=
-
8
x
x
2
+
4
的圖象，并探究其性質，列表如下：

x … -5 -4 -3 -2 -1 0 1 2 3 4 5 …

y …
40
29

8
5

24
13
2
8
5
0 m -2
-
24
13

-
8
5

-
40
29
…

（1）①根據表中數據，可知m=
-
8
5
-
8
5
；
②描點：根據表中的數值描點（x,y），請補充描出點（1，m）；
③連線：用平滑的曲線順次連接各點，請畫出函數圖象；
（2）探究函數性質請寫出函數y=
8
x
x
2
+
4
的兩條性質：①
當x=2時，函數有最小值，最小值為-2
當x=2時，函數有最小值，最小值為-2
；②
當1＜x＜1時，函數y的值隨x的增大而減小
當1＜x＜1時，函數y的值隨x的增大而減小
；
（3）運用函數圖象及性質根據函數圖象，寫出不等式
8
x
x
2
+
4
＞
x
解集是
x＜-2或0＜x＜2
x＜-2或0＜x＜2
．

【答案】-

；當x=2時，函數有最小值，最小值為-2；當1＜x＜1時，函數y的值隨x的增大而減小；x＜-2或0＜x＜2

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/25 21:30:1組卷：103引用：1難度：0.5

相似題

1．已知函數y=3x+1的圖象經過點A（
2
3
，m），則關于x的不等式3x＜m-1的解集為（　　）
A．x＜
3
2
B．x＜
2
3
C．x＞-
3
2
D．x＞-
2
3
發布：2025/5/25 15:0:2組卷：672引用：3難度：0.6
解析
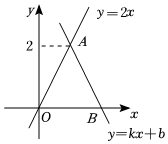2．如圖，函數y=kx+b（k≠0）的圖象經過點B（m,0）（m＞1），與函數y=2x的圖象交于點A，則不等式kx+b＜2x的解集為（　　）
A．x＞0 B．x＜1 C．x＞1 D．x＞2
發布：2025/5/26 0:0:1組卷：445引用：1難度：0.7
解析

3．探究函數性質時，我們經歷了列表、描點、連線畫出函數圖象，觀察分析圖象特征，概括函數性質的過程．結合已有的學習經驗，請畫出函數y=-
12
x
2
+
2
的圖象并探究該函數的性質．

x … -4 -3 -2 -1 0 1 2 3 4 …

y … -
2
3
a -2 -4 b -4 -2 -
12
11
-
2
3
…

（1）列表，寫出表中a,b的值：a=
，b=
；
描點、連線，在所給的平面直角坐標系中畫出該函數的圖象．
（2）觀察函數圖象，判斷下列關于函數性質的結論是否正確（在答題卡相應位置正確的用“√”作答，錯誤的用“×”作答）：
①函數y=-
12
x
2
+
2
的圖象關于y軸對稱；
②當x=0時，函數y=-
12
x
2
+
2
有最小值，最小值為-6；
③在自變量的取值范圍內函數y的值隨自變量x的增大而減小．
（3）已知函數y=-
2
3
x-
10
3
的圖象如圖所示，結合你所畫的函數圖象，直接寫出不等式-
1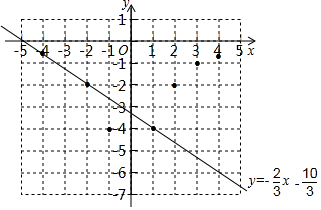2
x
2
+
2
＜-
2
3
x-
10
3
的解集．

發布：2025/5/25 16:0:2組卷：1775引用：15難度：0.6

相關試卷

x	…	-5	-4	-3	-2	-1	0	1	2	3	4	5	…
y	…	40 29	8 5	24 13	2	8 5	0	m	-2	- 24 13	- 8 5	- 40 29	…