 知識遷移
知識遷移
我們知道,函數(shù)y=a(x-m)2+n(a≠0,m>0,n>0)的圖象是由二次函數(shù)y=ax2的圖象向右平移m個單位,再向上平移n個單位得到;類似地,函數(shù)y=kx-m+n(k≠0,m>0,n>0)的圖象是由反比例函數(shù)y=kx的圖象向右平移m個單位,再向上平移n個單位得到,其對稱中心坐標(biāo)為(m,n).
理解應(yīng)用
函數(shù)y=3x-1+1的圖象可由函數(shù)y=3x的圖象向右平移11個單位,再向上平移11個單位得到,其對稱中心坐標(biāo)為(1,1)(1,1).
靈活應(yīng)用
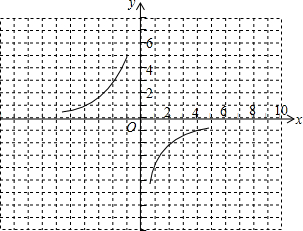
如圖,在平面直角坐標(biāo)系xOy中,請根據(jù)所給的y=-4x的圖象畫出函數(shù)y=-4x-2-2的圖象,并根據(jù)該圖象指出,當(dāng)x在什么范圍內(nèi)變化時,y≥-1?
實際應(yīng)用
某老師對一位學(xué)生的學(xué)習(xí)情況進(jìn)行跟蹤研究,假設(shè)剛學(xué)完新知識時的記憶存留量為1,新知識學(xué)習(xí)后經(jīng)過的時間為x,發(fā)現(xiàn)該生的記憶存留量隨x變化的函數(shù)關(guān)系為y1=4x+4;若在x=t(t≥4)時進(jìn)行第一次復(fù)習(xí),發(fā)現(xiàn)他復(fù)習(xí)后的記憶存留量是復(fù)習(xí)前的2倍(復(fù)習(xí)的時間忽略不計),且復(fù)習(xí)后的記憶存留量隨x變化的函數(shù)關(guān)系為y2=8x-a,如果記憶存留量為12時是復(fù)習(xí)的“最佳時機點”,且他第一次復(fù)習(xí)是在“最佳時機點”進(jìn)行的,那么當(dāng)x為何值時,是他第二次復(fù)習(xí)的“最佳時機點”?
k
x
-
m
k
x
3
x
-
1
3
x
-
4
x
-
4
x
-
2
4
x
+
4
8
x
-
a
1
2
【考點】反比例函數(shù)綜合題.
【答案】1;1;(1,1)
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:1317引用:48難度:0.5
相似題
-
1.已知反比例函數(shù)
(k>0)和矩形OABC.y=kx
(1)如圖若k=2,OA=2AB,如果B在反比例函數(shù)y=的圖象上,求B點坐標(biāo);kx
(2)如圖若k=2,OA=2AB,AB和BC交反比例函數(shù)y=(k>0)的圖象分別與N、M.求證:BN=2BM;kx
(3)如圖若AB和BC交反比例函數(shù)y=(k>0)的圖象分別與N、M;OA=kAB.求證:MN∥AC.kx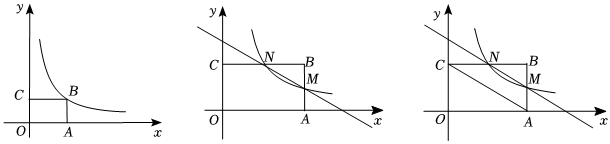 發(fā)布:2025/5/23 10:30:1組卷:129引用:1難度:0.4
發(fā)布:2025/5/23 10:30:1組卷:129引用:1難度:0.4 -
2.在平面直角坐標(biāo)系xOy中,一次函數(shù)y=k(x-1)+6(k>0)的圖象與反比例函數(shù)
的圖象的一個交點的橫坐標(biāo)為1.y=mx(m≠0)
(1)求這個反比例函數(shù)的解析式;
(2)當(dāng)x<-3時,對于x的每一個值,反比例函數(shù)的值大于一次函數(shù)y=k(x-1)+6(k>0)的值,直接寫出k的取值范圍.y=mx發(fā)布:2025/5/23 11:0:1組卷:758引用:5難度:0.3 -
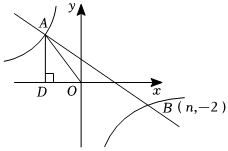 3.如圖所示,在平面直角坐標(biāo)系中,一次函數(shù)y=kx+b(k≠0)與反比例函數(shù)y=(a≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=8,sin∠AOD=ax,且點B的坐標(biāo)為(n,-2).45
3.如圖所示,在平面直角坐標(biāo)系中,一次函數(shù)y=kx+b(k≠0)與反比例函數(shù)y=(a≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=8,sin∠AOD=ax,且點B的坐標(biāo)為(n,-2).45
(1)求一次函數(shù)與反比例函數(shù)的解析式;
(2)請直接寫出滿足kx+b>的x的取值范圍;ax
(3)E是y軸上一點,且△AOE是等腰三角形,直接寫出所有符合條件的E點坐標(biāo).發(fā)布:2025/5/23 17:0:1組卷:365引用:2難度:0.3
相關(guān)試卷


