本學期我們研究了三角形的中位線的性質，回顧研究的過程，請回答以下問題：
（1）三角形中位線定理是：三角形的中位線平行于第三邊，且等于第三邊的一半三角形的中位線平行于第三邊，且等于第三邊的一半；
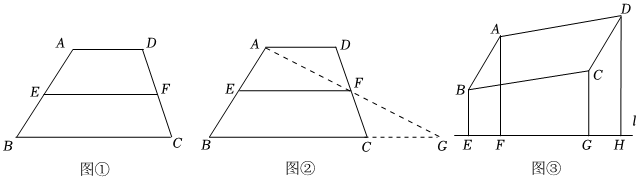
（2）梯形是有一組對邊平行，另一組對邊不平行的四邊形，連接梯形兩腰的中點，得到的線段叫做梯形的中位線．如圖①，EF就是梯形ABCD的中位線，梯形的中位線具有什么性質呢？
小明思考之后給出了如下的證明思路：
如圖②，連接AF并延長，交BC的延長線于點G．
先證△ADF和△GCF全等，再說明EF是△ABG的中位線．
…
經過你的分析，請寫出梯形的中位線EF和兩底AD、BC之間的關系：EF=12（AD+BC）EF=12（AD+BC）、EF∥AD∥BCEF∥AD∥BC；
（3）已知梯形的中位線長為7cm,高為6cm,則梯形面積是 4242cm2；
（4）如圖③，直線l為?ABCD外的任意一條直線，過A、B、C、D分別作直線l的垂線段BE、AF、CG、DH，請探索線段BE、AF、CG、DH之間的數量關系，并證明．
1
2
1
2
【考點】四邊形綜合題．
【答案】三角形的中位線平行于第三邊，且等于第三邊的一半；EF=（AD+BC）；EF∥AD∥BC；42
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/15 8:0:9組卷：183引用：1難度：0.5
相似題
-
1．點P是矩形ABCD的邊BC上一動點，連接AP、DP，將△ABP、△DCP分別沿AP、DP翻折，得到△AB'P、△DC'P．
（1）如圖1，PB'交AD于點M，PC'交AD于N，N在M的右側，求證：PM+MN+PN=AD；
（2）如圖2，當P、B'、C'共線時，稱點P為BC邊上的“疊合點”．
①在矩形ABCD中，AB=4，BC=10，點P為BC邊上的“疊合點”，求DP的長；
②若在矩形ABCD中，AD=4AB，點P是BC邊上的“疊合點”，則=．BPCP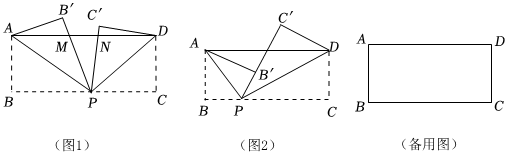
發布：2025/6/4 11:30:1組卷：310引用：1難度：0.4 -
2．如圖，點E是菱形ABCD對角線BD上一動點，BD=12．在線段BD的同側作線段DF=EC，使得∠CED=∠FDE，連接CF．
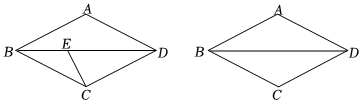
（1）補全圖形，并回答問題：當BE=時，DF⊥CF；
（2）連接AF，交BD于點G，若EC⊥CD，探索AG與BE的數量關系，并證明；
（3）直接寫出當BE=時，CE將平行AF．發布：2025/6/4 11:30:1組卷：134引用：2難度：0.3 -
3．如圖，正方形ABCD的邊長為1，將正方形ABCD繞點C順時針旋轉α到正方形A′B′CD′，其中0°＜α＜90°，AD與A′B′相交于點E．
（1）如圖1，求證：A′E=AE．
（2）如圖2，當E是AD中點時，
①請寫出AB′與B′D之間的關系，并證明；
②∠A′DD′=，當正方形ABCD的面積為36時，DD′的長為 ．
?發布：2025/6/4 11:30:1組卷：579引用：1難度：0.1