如圖，在△ABC中，∠C=90°，AB=5，AC=4，點P是AB的中點．動點M沿CB邊從點C開始，向點B以每秒1個單位長度的速度運動，當點M到達點B時停止運動，以點C為圓心，CM的長為半徑作圓，與AC交于點N，過點N作NQ⊥AB，垂足為點Q．設運動的時間為t秒．
（1）當⊙C與AB相切時，求t的值；
（2）用含t的代數式表示NQ的長；
（3）當⊙C與線段PQ有交點時，直接寫出線段NQ所掃過的面積．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：365引用：5難度：0.5
相似題
-
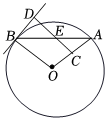1．如圖，AB是⊙O的一條弦，E是AB的中點，過點E作EC⊥OA于點C，過點B作⊙O的切線交CE的延長線于點D．
（1）求證：∠EBD=∠BED；
（2）若AB=24，BD=10，求⊙O的半徑．發布：2025/5/24 20:0:2組卷：29引用：1難度：0.7 -
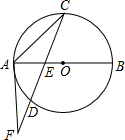2．如圖，AB是⊙O的直徑，弦CD與AB交于點E，過點A作⊙O的切線與CD的延長線交于點F，如果DE=CE，AC=34，D為EF的中點．85
（1）求證：∠AFC=∠ACF；
（2）求AB的長．發布：2025/5/24 19:30:1組卷：210引用：3難度：0.5 -
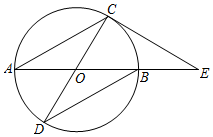3．如圖，AB、CD是⊙O的兩條直徑，過點C的⊙O的切線交AB的延長線于點E，連接AC、BD．
（1）求證：∠ABD=∠CAB；
（2）若B是OE的中點，AC=12，求⊙O的半徑．發布：2025/5/24 20:0:2組卷：6419引用：7難度：0.4