大家在學完勾股定理的證明后發現運用“同一圖形的面積不同表示方式相同”可以證明一類含有線段的等式，這種解決問題的方法我們稱之為面積法．學有所用：在等腰三角形ABC中，AB=AC，其一腰上的高為h,M是底邊BC上的任意一點，M到腰AB、AC的距離分別為h1、h2．
（1）請你結合圖形來證明：h1+h2=h；
（2）當點M在BC延長線上時，h1、h2、h之間又有什么樣的結論．請你畫出圖形，并直接寫出結論不必證明；
（3）利用以上結論解答，如圖在平面直角坐標系中有兩條直線l1：y=34x+3，l2：y=-3x+3，若l2上的一點M到l1的距離是32．求點M的坐標．
3
4
3
2
【考點】勾股定理的證明．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：10469引用：26難度：0.1
相似題
-
1．（1）為了證明勾股定理，李明將兩個全等的直角三角形按如圖1所示擺放，使點A、E、D在同一條直線上，如圖1，請利用此圖證明勾股定理；
（2）如圖2，△ABC中，∠ACB=90°，AB=10cm,BC=6cm,若點P從點A出發，以每秒4cm的速度沿折線A-C-B運動，設運動時間為t秒（t＞0），若點P在∠BAC的平分線上，求此時t的值．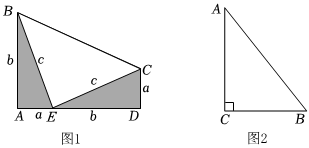
發布：2025/6/5 23:0:2組卷：477引用：7難度：0.7 -
2．勾股定理是人類最偉大的十個科學發現之一，西方國家稱之為畢達哥拉斯定理．在我國古書《周髀算經》中就有“若勾三，股四，則弦五”的記載，我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”（如圖①），后人稱之為“趙爽弦圖”，流傳至今．如圖①是用四個能夠完全重合的直角三角形拼成的圖形，其中直角邊長分別為a,b,斜邊長為c,用含a,b,c的代數式表示：
（1）大正方形的面積為 ；小正方形的面積為 ；
（2）四個直角三角形的面積和為 ，根據圖中面積關系，可列出a,b,c之間的關系式為 ；
（3）如圖②，以直角三角形的三邊為直徑，分別向外部作半圓，則S1，S2，S3滿足的關系是 ；
（4）如圖③直角三角形的兩條直角邊長分別為3、5，分別以直角三角形的三邊為直徑作半圓，則圖中兩個月形圖案（陰影部分）的面積和為 ．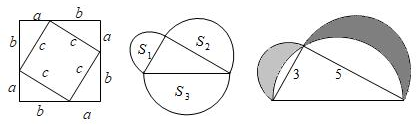
發布：2025/6/5 20:30:1組卷：208引用：2難度：0.4 -
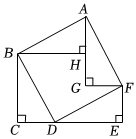3．如圖，由四個全等的直角三角形拼成的圖形，設CE=a,HG=b,則斜邊BD的長是（ ）發布：2025/6/5 21:30:1組卷：2346引用：8難度：0.7