【課本再現】
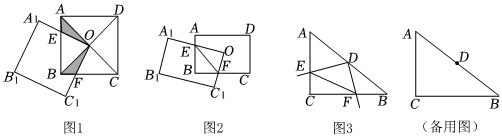
（1）如圖1，正方形ABCD的對角線相交于點O，點O又是正方形A1B1C1O的一個頂點，而且這兩個正方形的邊長都為1，四邊形OEBF為兩個正方形重疊部分．正方形A1B1C1O可繞點O轉動．則下列結論正確的是 ①②③④①②③④（填序號即可）．
①△AEO≌△BFO；
②OE=OF；
③四邊形OEBF的面積總等于14S正方形ABCD；
④連接EF，總有AE2+CF2=EF2．
【類比遷移】
（2）如圖2，矩形ABCD的中心O是矩形A1B1C1O的一個頂點，A1O與邊AB相交于點E，C1O與邊CB相交于點F，連接EF，矩形A1B1C1O可繞著點O旋轉，猜想AE，CF，EF之間的數量關系，并進行證明；
【拓展應用】
（3）如圖3，在Rt△ACB中，∠C=90°，AC=3cm,BC=4cm,直角∠EDF的頂點D在邊AB的中點處，它的兩條邊DE和DF分別與直線AC，BC相交于點E，F，∠EDF可繞著點D旋轉，當AE=2cm時，求線段EF的長度．
1
4
S
正方形
ABCD
【考點】四邊形綜合題．
【答案】①②③④
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/16 8:0:9組卷：491引用：8難度：0.5
相似題
-
1．“矩形的折疊”活動課上引導學生對矩形紙片進行折疊．
如圖，將矩形紙片ABCD折疊，點A與點D重合，點C與點B重合，將紙片展開，折痕為EF，在AD邊上找一點P，沿CP將△PCD折疊，得到△PCQ，點D的對應點為點Q．
問題提出：
（1）若點Q落在EF上，CD=2，連接BQ．
①△CQB是 三角形；
②若△CQB是等邊三角形，則AD的長為 ．
深入探究：
（2）在（1）的條件下，當AD=2時，判斷△CQB的形狀并證明；2
拓展延伸；
（3）若AB=6，AD=8，其他條件不變，當點Q落在矩形ABFE內部（包括邊）時，連接AQ，直接寫出AQ的取值范圍．發布：2025/5/22 16:30:1組卷：236引用：2難度：0.3 -
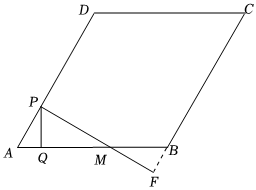2．如圖，在菱形ABCD中，AB=4，∠BAD=60°，點P從點A出發，沿線段AD以每秒1個單位長度的速度向終點D運動，過點P作PQ⊥AB于點Q，作PM⊥AD交直線AB于點M，交直線BC于點F，設△PQM與菱形ABCD重疊部分圖形的面積 為s（平方單位），點P運動時間為t（秒）．
（1）當點M與點B重合時，則t=；
（2）求整個運動過程中s的最大值；
（3）以線段PQ為邊，在PQ右側作等邊△PQE，當2≤t≤4時，求點E運動路徑的長．發布：2025/5/22 17:0:1組卷：407引用：5難度：0.3 -
3．已知二次函數y=mx2-（2m-1）x-2．
（1）求證：該函數圖象與x軸必有交點；
（2）當m＜0時，該函數圖象頂點的最低點坐標是（ ，）
（3）如圖，若點A（1，1）、B（3，1）、C（1，-1）、D（3，-1）四個點構成一個正方形方框，隨著m的變化，函數的圖象也不斷發生變化；此時圖象與方框的交點個數為n,請直接寫出n的值以及相應的m的范圍．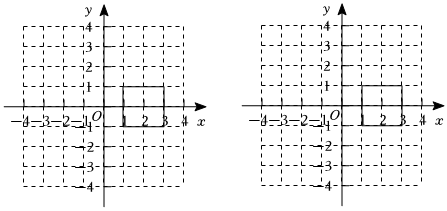
發布：2025/5/22 17:30:2組卷：249引用：1難度：0.1