[閱讀理解]
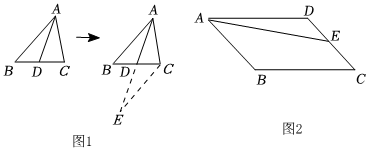
“倍長中線”是初中數(shù)學一種重要的思想方法．如圖1，在△ABC中，AD是BC邊上的中線，若延長AD至E，使DE=AD，連接CE，可根據(jù)SAB證明△ABD≌△ECD，則AB=EC．
[問題提出]
（1）如圖2，平行四邊形ABCD中，點E為CD邊的中點，在BC邊上找一點F，使得AF=AD+CF（要求：用直尺和圓規(guī)作圖，保留作圖痕跡，不寫作法）．
（2）按照你（1）中的作圖過程證明：AF=AD+CF．
【考點】四邊形綜合題．
【答案】（1）作圖過程見解答；
（2）證明過程見解答．
（2）證明過程見解答．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/9 15:30:2組卷：265引用：3難度：0.1
相似題
-
1．在一次數(shù)學研究學習中，小明將兩個全等的直角三角形紙片ABC和DEF拼在一起，使點A與點F重合，點C與點D重合（如圖1），其中∠ACB=∠DFE=90°，BC=EF=6cm,AC=DF=8cm,并進行如下研究活動．
活動一：將圖1中的紙片DEF沿AC方向平移，連接AE，BD（如圖2），當點F與點C重合時停止平移．
[思考]圖2中的四邊形ABDE是平行四邊形嗎？請說明理由．
[發(fā)現(xiàn)]當紙片DEF平移到某一位置時，小明發(fā)現(xiàn)四邊形ABDE為矩形（如圖3）．求AF的長．
活動二：在圖3中，取AD的中點O，再將紙片DEF繞點O順時針方向旋轉(zhuǎn)a度（0≤a≤90），連接OB，OE（如圖4）．
[探究]當EF平分∠AEO時，探究OF與BD的數(shù)量關(guān)系，并說明理由.
發(fā)布：2025/6/9 21:0:1組卷：144引用：2難度：0.2 -
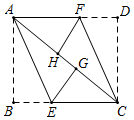2．【探究】在一次數(shù)學課上，老師出示了這樣一道題目：“如圖，在矩形ABCD中，AC：為對角線，AB＜AD，E、F分別為邊BC、AD上的點，連接AE、CF，分別將△ABE和△CDF沿AE、CF翻折，使點B、D的對稱點G、H都落在AC上，求證：四邊形AECF是平行四邊形．”以下是兩名學生的解題方法：
甲學生的方法是：首先由矩形的性質(zhì)和軸對稱的性質(zhì)證得AB=CD，AD∥BC，∠AHF=90°，∠CGE=90°，易得AH=CG，可得△AFH≌△CEG（ASA），由平行四邊形的判定定理可得結(jié)論．
乙學生的方法是：不利用三角形全等知識，依據(jù)平行四邊形的定義證明．
（1）甲學生證明四邊形AECF是平行四邊形所用的判定定理的內(nèi)容是．
（2）用乙學生的方法完成證明過程．
【應(yīng)用】當學生們完成證明后，老師又提出了一個問題：
若四邊形AECF是菱形，則tan∠DAC的值為．發(fā)布：2025/6/9 19:0:2組卷：248引用：5難度：0.3 -
3．【證明體驗】（1）如圖（1），在△ABC中，∠ACB=2∠ABC，AD平分∠BAC交BC于D，點E在AB上，AE=AC，連結(jié)DE，求證：EB=CD．
【思考探究】（2）如圖（2），在（1）的條件下，過點C作CF∥DE交AB于點F，交AD于點G，若AB=6，AC=4，求FG的長．
【拓展延伸】（3）如圖（3），在四邊形ABCD中，∠BAC=90°，且∠ABC=∠BDC=∠ACD，若AB=4，CD=12，求BD的長．103
發(fā)布：2025/6/9 19:30:1組卷：461引用：3難度：0.3