(1)若多項式x2-mx-8可分解為(x+2)(x+n),求m?n的值;
(2)已知(a+b)2=17,(a-b)2=5,求a2+b2,ab的值;
(3)在(2)的條件下求a4-a2b2+b4的值.
【考點】因式分解-十字相乘法等;因式分解-運用公式法.
【答案】(1)-8;(2)a2+b2=11,ab=3;(3)94.
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/6/7 10:30:1組卷:70引用:2難度:0.8
相似題
-
1.閱讀下列材料:
對于多項式x2+x-2,如果我們把x=1代入此多項式,發(fā)現(xiàn)x2+x-2的值為0,這時可以確定多項式中有因式(x-1);同理,可以確定多項式中有另一個因式(x+2),于是我們可以得到:x2+x-2=(x-1)(x+2).又如:對于多項式2x2-3x-2,發(fā)現(xiàn)當(dāng)x=2時,2x2-3x-2的值為0,則多項式2x2-3x-2有一個因式(x-2),我們可以設(shè)2x2-3x-2=(x-2)(mx+n),解得m=2,n=1,于是我們可以得到:2x2-3x-2=(x-2)(2x+1).
請你根據(jù)以上材料,解答以下問題:
(1)當(dāng)x=時,多項式8x2-x-7的值為0,所以多項式8x2-x-7有因式 ,從而因式分解8x2-x-7=;
(2)以上這種因式分解的方法叫試根法,常用來分解一些比較復(fù)雜的多項式,請你嘗試用試根法分解多項式:
①3x2+11x+10;
②x3-21x+20.發(fā)布:2025/6/6 19:30:1組卷:1137引用:7難度:0.6 -
2.在分解因式時x2+ax+b時,甲看錯了a的值,分解的結(jié)果是(x+1)(x+9);乙看錯了b的值,分解的結(jié)果是(x-2)(x-4).那么x2+ax+b分解因式正確的結(jié)果是多少?為什么?
發(fā)布:2025/6/7 16:0:2組卷:242引用:2難度:0.7 -
3.提出問題:你能把多項式x2+5x+6因式分解嗎?
探究問題:如圖1所示,設(shè)a,b為常數(shù),由面積相等可得:(x+a)(x+b)=x2+ax+bx+ab=x2+(a+b)x+ab,將該式從右到左使用,就可以對形如x2+(a+b)x+ab的多項式進(jìn)行因式分解即x2+(a+b)x+ab=(x+a)(x+b).觀察多項式x2+(a+b)x+ab的特征是二次項系數(shù)為1,常數(shù)項為兩數(shù)之積,一次項為兩數(shù)之和.
解決問題:x2+5x+6=x2+(2+3)x+2×3=(x+3)(x+2)
運用結(jié)論: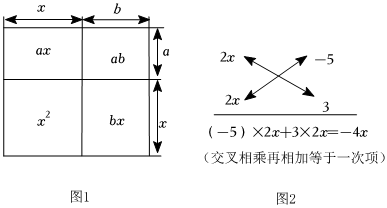
(1)基礎(chǔ)運用:把多項式x2-5x-24進(jìn)行因式分解;
(2)知識遷移:對于多項式4x2-4x-15進(jìn)行因式分解還可以這樣思考:
將二次項4x2分解成圖2中的兩個2x的積,再將常數(shù)項-15分解成-5與3的乘積,圖中的對角線上的乘積的和為-4x,就是4x2-4x-15的一次項,所以有4x2-4x-15=(2x-5)(2x+3).這種分解因式的方法叫做“十字相乘法”.請用十字相乘法進(jìn)行因式分解:3x2-19x-14.發(fā)布:2025/6/7 21:30:1組卷:115引用:1難度:0.7


