在等邊△ABC中，線段AM為BC邊上的中線．點D在直線AM上，以CD為一邊在CD的下方作等邊△CDE，連接BE．
（1）當(dāng)點D在線段AM上時，
①請在圖1中補全圖形；
②∠CAM的度數(shù)為 30°30°；
③求證：△ADC≌△BEC．
（2）當(dāng)點D在直線AM上時，直線BE與直線AM的交點為O（點D與點M不重合，點E與點O不重合），直接寫出線段OE，OM，DM與BE的數(shù)量關(guān)系．
【答案】30°
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/27 7:0:1組卷：204引用：4難度：0.5
相似題
-
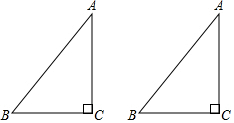1．下面是小宇設(shè)計的“作已知直角三角形的中位線”的尺規(guī)作圖過程．
已知：在△ABC中，∠C=90°．
求作：△ABC的中位線DE，使點D在AB上，點E在AC上．
作法：如圖，
①分別以A，C為圓心，大于AC長為半徑畫弧，兩弧交于P，Q兩點；12
②作直線PQ，與AB交于點D，與AC交于點E．
所以線段DE就是所求作的中位線．
根據(jù)小宇設(shè)計的尺規(guī)作圖過程，
（1）使用直尺和圓規(guī)，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：連接PA，PC，QA，QC，DC，
∵PA=PC，QA=，
∴PQ是AC的垂直平分線（）（填推理的依據(jù)）．
∴E為AC中點，AD=DC．
∴∠DAC=∠DCA，
又在Rt△ABC中，有∠BAC+∠ABC=90°，∠DCA+∠DCB=90°．
∴∠ABC=∠DCB（）（填推理的依據(jù)）．
∴DB=DC．
∴AD=BD=DC．
∴D為AB中點．
∴DE是△ABC的中位線．發(fā)布：2025/5/21 17:30:1組卷：139引用：4難度：0.5 -
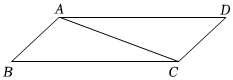2．如圖，在平行四邊形ABCD中，∠B=40°，∠ACD=120°．
請用尺規(guī)作圖法，在BC上求作一點E，使得∠CAE=80°．（保留作圖痕跡，不寫作法）發(fā)布：2025/5/21 16:0:1組卷：155引用：2難度：0.7 -
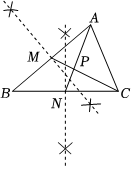3．如圖，已知△ABC的面積為12，結(jié)合尺規(guī)作圖痕跡所提供的條件可知，△APC的面積為 ．發(fā)布：2025/5/21 18:0:1組卷：90引用：2難度：0.5
相關(guān)試卷